Поєднання об'єктної і реляційної систем активно обговорюється в пресі - спектр думок надзвичайно широ, починаючи з ідеї про практичну ідентичності даних моделей, що вимагає лише незначного розширення однієї з них, і закінчуючи явним протиставленням, який веде до висновку про неможливість їх об'єднання. Критиці в тій чи іншій мірі піддаються обидві моделі.
ІТ-інфраструктура для вашого підприємства
Поєднання об'єктної і реляційної систем активно обговорюється в пресі - спектр думок надзвичайно широ, починаючи з ідеї про практичну ідентичності даних моделей, що вимагає лише незначного розширення однієї з них, і закінчуючи явним протиставленням, який веде до висновку про неможливість їх об'єднання. Критиці в тій чи іншій мірі піддаються обидві моделі.
Не вдаючись в подробиці можна сказати, що недоліки кожної моделі нерозривно пов'язані з їх перевагами і фактично протилежні одна одній. Реляційні системи (R-системи) критикуються за відсутність гнучкості, що є наслідком формальних (а отже, строгості і стабільності), а об'єктні (O-системи) - за відсутність формальності, що є наслідком гнучкості. [1,6,7,8, 19,21,22,23]
Дана робота виходить з практичної завершеності як реляційної так і об'єктної концепцій. Мета даної статті - показати, що ці концепції абсолютно не суперечать один одному і не потребують будь-яких змін для того, що б використовуватися в загальній системі, яка має всі властивості як об'єктних, так і реляційних систем.
Це ідея грунтується на наступних твердженнях:
- Один і той же набір даних може одночасно описуватися декількома різними моделями
- Реляційна і Об'єктна моделі - різні моделі.
- Структуру будь-якої складності можна нормалізувати.
Розглянемо ці твердження докладніше
Один і той же набір даних може одночасно описуватися різними моделями
Що ж можна розуміти під різними моделями даних? Можна розглянути це питання з точки зрненія класифікації моделей даних. В даний час виділяють три рівня моделювання прикладної області - концептуальний, логічний і фізичний [18,20]. У наведеному прикладі можна виділити моделі концептуального рівня (об'єктна модель мови C ++) і фізичного рівня (модель ОЗУ). Таким чином, можна припустити, що різними є моделі відносяться до різних рівнів. Однак таке визначення є досить умовним.
Більш строго різними моделями даних можна назвати ортогональні моделі. Визначення ортогональних моделей є вельми нетривіальним. В рамках даної статті цікавим видається наслідок ортогональності (засноване на тому, що модель даних можна визначити як безліч можливих типів даних [2]): будь-який тип даних визначений у моделі М * ортогональної даної моделі М, може розглядатися в даній моделі М тільки як скалярний (базовий) тип [6,8,10,12, 13,15]. У наведеному прикладі такими скалярними типами, використовуваними в об'єктної моделі мови С ++, є базові типи int, char і т.п. описують можливі типи елементів сховища даних, тобто визначені в моделі ОЗУ. Таким чином можна сказати, що один і той же набір даних може одночасно описуватися декількома ортогональними моделями.
Реляційна і об'єктно моделі - різні моделі
Реляційна і об'єктна моделі відносяться до різних рівнів моделювання прикладної області. Реляційна модель відноситься до логічному рівню моделювання, об'єктна модель є концептуальною. Для того щоб більш чітко визначити різницю між цими моделями розглянемо системи, засновані на них.
Системою можна назвати безліч закономірностей визначають існування і взаємодія елементів цієї системи. Для того, щоб описати якусь систему, введемо такі операції.
- Операція ADR (X) (де X - елемент системи) є необхідною і достатньою для однозначної ідентифікації елемента Х системи, тобто ADR (Xi)! = ADR (Xj) (при Xi! = Xj) і ADR (Xi) = ADR (Xj) (при Xi = Xj). Повертає величину необхідну для однозначної ідентифікації елемента X.
- Операція IS (X) повертає тип елемента Х. Оскільки тип можна визначити як безліч імен атрибутів, то можна сказати, що в системі існує якесь безліч є об'єднанням всіх множин імен атрибутів всіх типів, яке в подальшому будемо називати простором визначення типів. Таким чином операція IS (X) проектує елемент X на простанство визначення типів.
Слід сказати, що в загальному випадку простір визначення типів О-системи є складним і багатовимірним, що випливає з многобразие способів тіпообразованія в цій системі. [5,18] Одним з цих способів є успадкування. Цей спосіб притаманний тільки О-системам і дозволяє при визначенні нових типів використовувати вже існуючі, більш загальні за змістом, базові типи. Завдяки спадкоємства в О-системах один і той же атрибут може бути визначений в різних типах. На іллюстаціі клас В є спадкоємцем класу А і тому атрибут I визначений у класі А визначено також і в класі-спадкоємця В. [1,5,16]
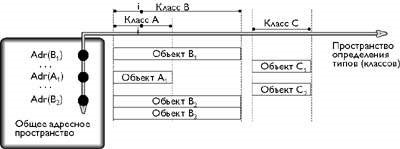
Мал. 1. Найпростіша реалізація O-системи
Для того щоб зобразити простір R-системи необхідно згадати про ключе.Ето поняття є одним з основних для R-систем і визначається наступним чином: ключем відносини називають таке підмножина всередині безлічі імен атрибутів відносини, що кортежі відносини можуть бути однозначно визначені значеннями відповідних атрибутів цього підмножини. Таким чином ключ складається з набору значень які однозначно визначають будь-який рядок таблиці. Певне значення ключового поля (або полів), що належать записи деякої таблиці, дозволяє знайти цей запис всередині цієї таблиці. [1,4]
Для однозначної ідентифікації кортежу Х деякого відносини R операція ADR (X) повинна повернути вираз виду (R, K), яке звучить як «Ключ K кортежу X відносини R де R = IS (X)». На цьому визначенні грунтується поняття зовнішнього ключа, який може бути названий R-аналогом посилань і покажчиків O-систем. Визначення подібного роду дозволяє ввести в R-системи (рис. 2) механізм підтримки посилальної цілісності який дозволить привласнити посиланням (зовнішньому ключу) значення виходить з області значень первинного ключа відповідного ставлення.
Якщо порівнювати простору R- і O- систем то можна відзначити дві відмінності:
2. У просторі визначення типів: рис.1 ілюструє успадкування - одне з ключових понять O-систем. На малюнку клас B є спадкоємцем класу А.
Основні властивості системи, що об'єднує R- і O- системи, повинні складатися з властивостей притаманних кожній з цих систем окремо. отже
- всі дані, наявні в такій системі повинні бути представлені як об'єкти прозвольной структури.
- всі дані, наявні в такій системі повинні бути представлені у вигляді реляційних змінних [9]
Ці міркування приводять нас до введення в R-систему поняття RecID - ідентифікатора, що дозволяє однозначно визначити будь-який кортеж системи. Слід зауважити, що поле містить RecID є ключовим для будь-якої таблиці хоча може бути і не визначено явно як ключ.
Введення RecID не представляє особливої складності. Сенс, однак, полягає не в самому RecID. Важливим є можливість використовувати його значення для ініціалізації посилань (або покажчиків), які дозволяють іншим частинам системи звертатися до даного кортежу. Можна розглянути два випадки:
Застосування успадкування для відносин
Погляньмо ще раз на рис. (1) описує простір O-системи. Клас B є спадкоємцем класу А. Таким чином для операції IS (Bi) (де Вi - об'єкт класу B) можливі два варіанти правильної відповіді - клас А і клас В. Можна сказати, що IS (Bi) = IS (Aj) в то час як IS (Ai)! = IS (Bj). Ця закономірність є наслідком гнучкості O-систем в їх здатності визначати нові типи.
Однак, оскільки різні моделі можуть одночасно використовуватися для опису одного і того ж набору даних, можна припустити, що для цього можуть використовуватися реляційна і об'єктна моделі. Для цього ці моделі слід розглядати як ортогональні. І для того, що б співвіднести ці моделі згадаємо про те, що
Структуру будь-якої складності можна нормалізувати
Для того щоб зрозуміти що мається на увазі, повернемось до нашого прикладу з програмою зберігає свої дані в ОЗУ. Ми можемо сказати, що в ОЗУ може бути збережена будь-яка інформація (у всякому разі до цих пір це вдавалося). Соответсвенно інформація про деяке моделюється об'єкті (тут ми виходимо з того, що будь-яка програма в тій чи іншій мірі є способом моделювання якоїсь предметної області) представляє з себе деякий безліч елементів ОЗУ. Важливим є той факт, що це вірно для будь-якої програми, будь вона написана на Сі, FORTRAN або асемблері (всі ці мови використовують різні парадигми програмування і не є об'єктними) - в будь-якому випадку деякого модельованого об'єкту можна поставити у відповідність деякий безліч елементів ОЗУ, зберігають дані про цей об'єкт. Перевага об'єктних систем полягає в тому, що тільки вони дозволяють явно поставити в відповідність об'єкту моделюється області можуть бути ідентифіковані осмислено (або, по іншому, ЯКИЙ МАЄ ПЕВНУ СТРУКТУРУ) набір елеметов ОЗУ, який також (в термінах О-систем) називається об'єктом.
Аналогічні міркування вірні і для об'єкта, дані про який необхідно зберегти в реляційної базі даних. З того факту, що інформація про об'єкті з довільної внутрішньою структурою може бути збережена в реляційної системі, необхідно зробити наступний висновок: будь-якого об'єкта можна поставити у відповідність можуть бути ідентифіковані осмисленні набір кортежів.
Розглянемо це положення по частинах:
1) об'єкт є ідентифікований набір кортежів. Набору кортежів містить дані про деякий об'єкт можна поставити у відповідність унікальний ідентифікатор, який фактично є об'єктним ідентфікатором (OID), використовуючи який ми можемо звертатися до даного набору кортежів;
2) об'єкт є осмислений набір кортежів. Об'єкт описується типом, кожному атрибуту якого ставитися я у відповідність певне семантичне значення. Це семантичне значення визначає зміст кортежу в об'єкті і, крім того, позвляет звертатися до цього кортежу як до атрибуту об'єкта.
Дуже важливо розуміти, що мова тут йде про сенс, який притаманний кортежу як атрибуту об'єкта. Справа в тому, що будь-який кортеж може володіти власним змістом, і цей сенс визначається відношенням до якого цей кортеж входять. Кортеж сам по собі є семантично значущим набором даних. І цей осмислений набір даних осмислений також в контексті об'єкта, атрибутом якого він є. У цьому немає ніякого протиріччя. Розглянемо наступний приклад.
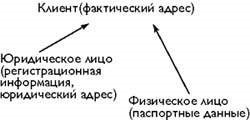
У нашому прикладі ми маємо справу і з класами (об'єктна модель) і з відносинами (реляційна модель). Оскільки об'єктна і реляційна моделі можуть рассмарівается тільки як ортогональні, цей приклад може бути проілюстрований наступним чином (рис. 4)
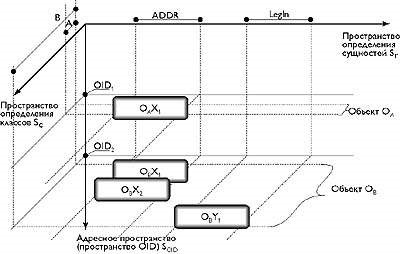
Мал. 4. R * O-система