Розвиток просторових уявлень - одна з найважливіших цілей шкільної освіти. Досвід показує, що в учнів 5-х класів вже досить сформовані початкові просторові уявлення, пов'язані з їх життєвим досвідом і предметами навколишньої дійсності. Діти "живуть" в просторовому світі, вважають площину геометричною фігурою, непогано читають креслення, багато вміють зображувати просторові фігури, фантазують, хоча оперувати уявними образами вони не вміють. У 5-6 класах також є можливості для формування початкових просторових уявлень. Однак до кінця вивчення курсу планіметрії учні 9-х класів вже міцно "прив'язані" до площини, вважали її геометричною фігурою, а місцем, на якому розташовані плоскі фігури.
Це говорить про те, що просторове мислення учнів 9 класів придушене, тому що увага дітей штучно затримується на планіметрії. У зв'язку з цим доцільно проводити на уроках геометрії вивчення планіметричних питань із залученням стереометричного матеріалу, або паралельно з традиційним курсом планіметрії проводити факультативні заняття, значно розширюють коло досліджуваних фігур і їх властивостей.
Пропонований урок геометрії можна провести в 7-9 класах.
1. Розвивати просторове мислення.
3. Вчити правильно зображати просторові фігури.
4. Виховувати графічну культуру учнів.
устаткування:- Мультимедійний проектор, екран або інтерактивна дошка, комп'ютер.
- Презентація уроку.
- Моделі пірамід, призм, циліндра, конуса, в тому числі каркасні.
- Картонний коло, пофарбований в яскравий колір.
- Мензурки на кожен стіл.
- Розчин марганцівки в великих циліндричному і конічному судинах.
1. Розглянути і проаналізувати готовий креслення.
2. Розглянути найпростіші геометричні тіла, вивести правила їх зображення, накреслити ці тіла.
3. Застосувати свої знання для самостійного побудови креслень.
4. Ознайомитися з поняттям перетину.
1. Організаційний момент.
2. Усна робота.
Ця частина уроку направлена на розширення загальних стереометричних уявлень і розвиток просторового мислення учнів. Важливо використовувати моделі фігур, їх креслення і уявні образи. Саме перехід від просторових образів реальних об'єктів до їх умовно-графічних зображень, від тривимірних зображень до двомірним і назад, тобто постійне перекодування образів і є просторове мислення.
- Що таке площину? Наведіть приклади площині в кабінеті.
- Скільки площин існує в просторі?
Діти повинні засвоїти, що площина - це така ж геометрична фігура, як і вже знайомі їм багатокутники, коло і т.д. і що площин, розташованих в різних положеннях, існує незліченна безліч. Можна змоделювати площину за допомогою підручника або зошити, зазначивши ще раз, що це тільки частина площині, сама ж площину - нескінченна.
- Що за постать зображена <рисунок1>? (Слайд3).
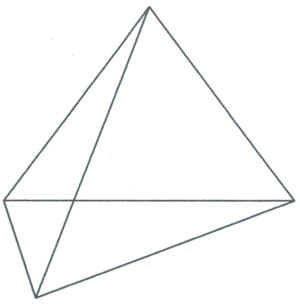
Креслення повинен бути саме таким, без пунктирних ліній. Діти повинні побачити не тільки чотирикутник, а й чотирикутну піраміду "зверху", трикутну піраміду "прозору".
- Яка піраміда зображена? (Чотирикутна, трикутна)
- Яка фігура лежить в її основі?
Діти повинні побачити звичні "плоскі" фігури в складі об'ємних.
- Які геометричні фігури ви знаєте?
Необхідно, щоб учні називали не тільки плоскі фігури, але і об'ємні.
- Назвіть геометричні тіла.
Учитель показує модель, діти називають.
3. Зображення фігур.
- Креслити плоскі фігури - трикутники, чотирикутники, і т.д. - ми вміємо. А як креслять об'ємні фігури?
- Що таке проектування (пояснення вчителя).
Показати на прикладі тіні, що відкидається на екран каркасної моделлю трикутної піраміди. Зображення тіні перенести на дошку.
- Чим незручно таке зображення? (Здається, що відрізки перетинаються, хоча насправді - немає; незрозуміло, що зображено)
- Правило: Лінії, які на звичайному малюнку фігури <рисунок2> (Слайд 4) не видно, креслимо пунктирною лінією (слайд 5).
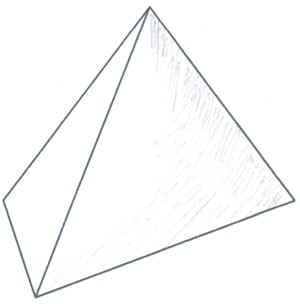
Розібрати на моделі, які лінії передаються в незмінному вигляді, а які - спотворюються.
- Властивості проекції (учитель сам називає ці властивості, або при наявності часу, діти можуть їх вивести):
1. Зберігається паралельність прямих.
2. проекцією середини відрізка є середина його проекції (слайд 6).
- Як накреслити правильну чотирикутну піраміду?
а) підстава (в яку фігуру переходить квадрат?);
б) діагоналі підстави;
в) висота (через точку перетину діагоналей);
г) бічні ребра.
Креслення підписати ( "чотирикутна піраміда").
- Як правильно накреслити правильну трикутну піраміду?
До дошки викликається учень.
Підстава переходить в неравнобедренний трикутник. Діти повинні зробити висновок, де знаходиться підставу висоти: висоту проводимо через точку перетину медіан. Розібрати, чому будуємо саме медіани - по властивості проекції №2. Креслення підписати "трикутна піраміда".
- Як накреслити прямий круговий циліндр?
Що в основі циліндра? Як буде виглядати підставу на кресленні? Проводиться досвід з картонним колом: спочатку вчитель тримає коло у вертикальній площині, потім повертає навколо горизонтального діаметра <рисунок3>. У що проектується коло? (В еліпс).
Учитель креслить разом з дітьми: мала піввісь в 2 рази менше великий. Креслення підписати "циліндр".
- Як побудувати конус?
До дошки викликається учень.
4. Побудова перетинів.
- Що таке перетин? (Пояснення вчителя).
- Що може вийти при перетині кулі площиною? (Приклад: кавун розрізають на дві частини).
Цей висновок учні повинні зробити без креслення і моделі.
- Що може вийти в перерізі циліндра?
Досвід з марганцівкою в мензурки. Налити кожному учневі в мензурку трохи розчину. Отримуємо коло. Нахиляємо мензурку. Отримуємо еліпс або його частину <рисунок4>. У зошитах на двох зображеннях циліндра намалювати різні види перетинів (слайд 7).
- Що може вийти в перерізі конуса? (Досвід з марганцівкою в конусоподібному посудині).
Звернути увагу: незважаючи на те, що верхня частина конуса має менший радіус кривизни, в перерізі виходить еліпс з однаковим радіусом кривизни у верхній і нижній частинах <рисунок5>. Будувати креслення в зошитах необов'язково (слайд 8).
- Що може вийти в перетині піраміди? (Багатокутники).
Учитель показує на готових кресленнях <рисунок6> (Слайд 9).
5. Самостійна робота.
За варіантами.- Варіант I. Побудувати паралелепіпед.
- Варіант II. Побудувати трикутну призму в вертикальному положенні.
- Варіант III. Побудувати трикутну призму в горизонтальному положенні. Каркасні моделі поставити на демонстраційний стіл.
6. Підведення підсумків уроку.