- Батурова Владлена Михайлівна. координатор експериментальної та інноваційної діяльності, вчитель початкових класів
В УМК «Початкова школа 21 століття» з предмету «Математика» передбачено програмою освоєння учнями широкого кола питань з геометрії. Уроки геометрії викликають у учнів стабільно високий пізнавальний інтерес. Незважаючи на те, що перед учителем не стоїть завдання обов'язкового засвоєння всіма учнями знань з геометрії в повному обсязі, можна сказати, що учні мого класу успішно опановують цим матеріалом.
Урок - перший по темі «Пряма» з трьох уроків. (Тип уроку - урок засвоєння нових знань.) Математичне визначення прямої для третьокласників складно. Тому в курсі геометрії для нас поняття «пряма» вводиться без визначення. Для учнів пряма - це лінія, яка проводиться по лінійці. Оскільки до цього уроку в учнів уже сформоване уявлення про промені, я вводжу поняття про прямий, спираючись на відомий факт, що промінь є нескінченною фігурою.
Особливості уроку геометрії визначають особливості введення нового матеріалу і засвоєння його: це відбувається не ДО практичної роботи учнів, а безпосередньо в процесі її. Вивчаючи особливості прямої як геометричної фігури, учні, користуючись засвоєними знаннями про промені, освоюють зону свого найближчого розвитку, діючи разом з учителем в єдиному інформаційному просторі уроку.
Мета: сформувати в учнів уявлення про особливості прямої як геометричної фігури.
устаткування:- Для учнів:
- плакат з латинськими літерами;
- кутник, лінійка;
- аркуші паперу для креслення;
- робочі зошити на друкованій основі;
- підручник.
- Для вчителя:
- на дошці - таблиця з зашифрованою темою уроку;
- на дошці - таблиця з кодом для дешифрування;
- кутник;
- лінійка.
Виконуючи завдання, учні повинні розшифрувати тему уроку. Букви і цифри таблиць закриті аркушами паперу. Право відкрити букву належить тому, хто першим назве приклад з таблиці множення із заданим відповіддю.
3. Введення в тему уроку. Активізація знань учнів
Отже, тема уроку перед вами.
- Що таке пряма? Що ми вже знаємо про неї? (Вона складається з точок, не має початку і кінця, може служити віссю симетрії будь-якої геометричної фігури.)
- Чи є у вас деякі припущення про те, як народилася ця фантастична особливість прямої - її нескінченність. Звідки вона взялася? (Діти висловлюють свої припущення.)
- Зараз на ваших очах відбудеться народження нескінченності прямий.
- Як називається ця фігура? (Луч ОВ)

- Що являє собою постать ОА? (Луч.)

- У нас вийшла фігура, яку називають ... пряма. На моєму малюнку пряму становлять які фігури? (Промені ОВ і ОА).
- Покажіть ці промені.
- Звідки ж з'явилася нескінченність прямої? Завдяки чому? (Тому, що пряму утворюють промені, які не мають кінця.)
- Що є спільне у цих двох променів? (Початок.)
- У яких напрямках повинні розташовуватися промені, щоб утворити пряму? (В протилежних.)
- Як найпростіше накреслити пряму, що не зображуючи складові її промені?
Накреслимо за допомогою лінійки кілька прямих, я - на дошці, а ви - в зошиті. Прямі можна проводити в різних напрямках.

- Як правильно показати пряму?
Оскільки пряма нескінченна в обидві сторони, то всю пряму, як і промінь, не можна накреслити на дошці або в зошиті і показати указкою. Кожен промінь має початок. Згадайте, як я вчила вас показувати промінь у 2 класі. Покажіть промінь ОВ на цьому малюнку. (Учень показує, встановлюючи указку в точку початку променя і проводячи по його зображенню, виходячи за його рамки.)
- Дякуємо. Але як же показати пряму, адже у неї немає початку? (Припущення дітей.)
- Домовимося: починаємо рух указкою видали (можна зліва направо або справа наліво); ведемо указкою по зображенню прямий і далі просуваємо її трохи далі (показую).
- У мене на дошці, а у вас в зошитах зображено кілька прямих. Як нам відрізнити одну пряму від іншої? (Припущення дітей.)
- Для цього пряму позначають буквами, записуючи їх над або під прямий. Літери повинні стояти рівно, вертикально. При цьому порядок читання букв не має значення: можна прочитати «пряма МА» або «пряма АМ».
- Позначимо кожну пряму на малюнку буквами латинського алфавіту. (Для останніх двох прямих учні самостійно вибирають назви).
Належність даних точок даної прямої
- Часто в геометрії нам доводиться з'ясовувати питання, чи лежить дана точка на даній прямій. Розгляньте малюнок на дошці.
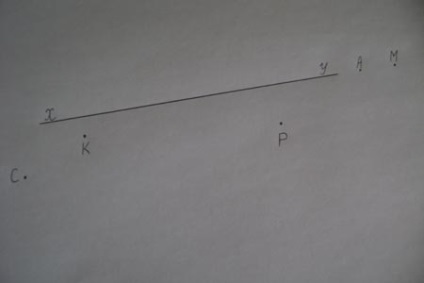
- що не лежать на даній прямій;
- що лежать на даній прямій.
- Доведіть, обґрунтуйте свою думку. За допомогою якого інструменту ми можемо довести, що точки A і M лежать на прямій XY? (За допомогою лінійки.)
- Покажіть, як це робити?
4. Закріплення нових знань
Підручник, с.37, №157.
- Прочитайте питання, розгляньте малюнок. Дайте відповідь. Доведіть свою думку.
- Послухайте, як на це питання відповів учень 3 класу однієї з московських шкіл: «Точки Е і С не лежать на прямій. Ось якщо ми продовжимо пряму, то вони будуть лежати на цій прямій ». Чи згодні ви з цією відповіддю? Які зауваження у вас є? Що, на вашу думку, не знає цей учень? (Відповіді дітей, обговорення.)
Висновок: безглуздо «продовжувати» пряму в ту чи іншу сторону, тому що пряма сама по собі нескінченна.
- Визначте спочатку на око, в якому із завдань прямі при перетині утворюють прямий кут. Перевірте себе за допомогою кутника.
- Якщо при перетині двох прямих ми виявили один прямий кут, то якими в цьому випадку будуть три залишилися кута? (Припущення.)
- Давайте перевіримо наші припущення. За допомогою якого інструменту це можна зробити? (Косинці.)
- Який ми можемо зробити висновок? Якщо при перетині двох прямих утворюється один прямий кут, то і інші три кути будуть прямими.
- Хлопці, в цьому випадку прийнято говорити, що «прямі перетинаються під прямим кутом». Повторіть цю фразу.
1) Побудуйте в зошиті дві прямі, які перетинаються під прямим кутом. Перевірка біля дошки на клітинної разлиновке. Що допомогло вам виконати це завдання? (Клітини в зошиті, тому що вони прокреслені під прямим кутом.)
2) Побудуйте на альбомному аркуші дві прямі, що перетинаються під прямим кутом. Як це треба робити, хто може пояснити і показати на дошці? Яким креслярським інструментом треба скористатися? (Кутником.)
№159. На яких малюнках прямі перетинаються, а на яких не перетинаються?
Поясніть, чому ви так вважаєте. (Йде обговорення можливих варіантів. Особливої уваги вимагає останній випадок розташування прямих, коли утворюються чотири променя - для розуміння цього в учнів повинно вже сформуватися уявлення про нескінченність прямої.)
5. Підведення підсумків
- Яке фантастичне властивість прямої?
- Як позначається пряма?
- Який інструмент потрібен, щоб зобразити дві прямі, що перетинаються під прямим кутом, на альбомному аркуші?
6. Оцінка роботи учнів на уроці
7. Інструктаж по домашньому завданню. Р / т №2 с.19-20 № 66-70
Необхідно відзначити, що плановані результати уроку були досягнуті. Це проявилося на етапі закріплення ЗУН, коли отримані ЗУН необхідно було комплексно застосувати для виконання завдань. У учнів протягом всього уроку спостерігався високий пізнавальний інтерес до занять, учні висловлювали вільно свої припущення, брали участь в їх обговоренні, висували нестандартні ідеї, використовували незвичайні порівняння, наприклад, порівняння зображення прямої зі стібком на тканини з лицьового і виворітного боку. Все це свідчить про те, що в учнів сформувалося уявлення про особливості прямої як геометричної фігури, тобто мета уроку була досягнута.