називається безперервної кусочно-гладкою, якщо функції безупинні на і відрізок можна розбити на кінцеве число часткових відрізків точками
так, що на кожному з них функції мають безперервні похідні, одночасно не рівні нулю.
На рис. 64 зображена безперервна кусочно-гладка крива. В точках і вона неперервна, але похідні всі або деякі терплять розрив (першого роду!).
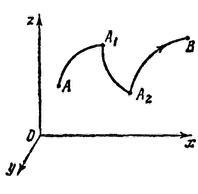
Криву (1) будемо позначати однією літерою, наприклад буквою. Зазвичай позначає не тільки геометричне місце точок, що визначаються рівнянням (1), але і порядок проходження цих точок, коли безперервно зростає від до. У цьому сенсі говорять, що є орієнтована крива. Порядок проходження позначають на малюнку стрілкою (рис. 64) - коли безперервно зростає від до, точка рухається по в напрямку стрілки.
Якщо є функція, що має безперервну позитивну похідну на деякому відрізку і при цьому, то рівняння
визначає ту ж орієнтовану криву, що і. Її позначають тією ж буквою, тільки говорять в разі рівняння (1), що визначається параметром, а в разі (1 ') - параметром. В обох випадках при зростанні від до або зростанні від до відповідні точки рухаються в одному і тому ж напрямку.
Інша справа, якщо зробити заміну, де має безперервну негативну похідну на відрізку. В цьому випадку, і при безперервному зростанні від до параметр буде спадати і стрілку на нашому геометричному об'єкті доведеться направити в інший бік.
Тому криву (1 ') в разі, коли, ми будемо позначати іншим символом і говорити, що є та сама крива, хто і, але орієнтована в протилежну сторону. Іноді вихідну орієнтовану криву ми будемо позначати символом.
Орієнтована крива (1) називається замкнутої або замкнутим контуром, якщо або, що все одно, якщо
Інакше кажучи; коли значення параметра безперервно зростає від до, відповідна точка проходить в просторі безперервний шлях, що починається і кінчається в одній і тій же точці. Якщо при цьому крива в інших точках сама себе не перетинає, то вона називається замкнутої самонепересекающейся кривої. На рис. 65, а зображена замкнута самонепересекающаяся крива, а на рис. 65, б - замкнута самопересекающиеся крива.

Зауваження. Векторне рівняння (1) кривої еквівалентно трьом рівнянням
Приклад 1. Нехай крива задана рівнянням
Так як, то дана крива є коло радіуса з центром в початку координат. При зростанні від 0 до точка рухається по колу проти годинникової стрілки. При цьому різним відповідають різні точки. При і маємо. Значить, окружність є замкнутої самонепересекающейся кривої (рис. 66).
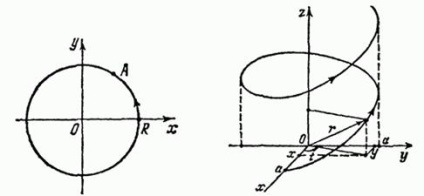
Приклад 2. Крива
де - позитивні числа, називається гвинтовою лінією. Її можна отримати наступним чином. Відрізок довжини, перпендикулярний осі, одним кінцем ковзає по осі і одночасно повертається близько осі, тоді інший кінець відрізка описує гвинтову лінію. Ми вважаємо, що висота підйому відрізка по осі пропорційна куту повороту. При зростанні точка рухається, як зазначено на рис. 67. Очевидно, що гвинтова лінія розташована на бічній поверхні кругового циліндра радіуса, з котра утворює, паралельної осі.