Білоруський ГОСУДРАСТВЕННИЙ університет інформатики і радіоелектроніки
Кафедра інженерної графіки
«Вигин прямолінійного стержня»
Загальні поняття про деформації вигину
Вигин викликається (рис. 1, а) зовнішніми силами, спрямованими перпендикулярно поздовжньої осі стержня, а також парами зовнішніх сил, площина дії яких проходить через цю вісь. При дії такого навантаження поздовжня вісь стрижня викривляється. У поперечних перетинах стрижня при вигині виникають моменти внутрішніх сил, площина дії яких перпендикулярна площині перетину, тобто згинальні моменти Мі.
Якщо згинальний момент в поперечному перерізі є єдиною складовою внутрішніх сил, вигин називається чистим.
Вигин називають поперечним, якщо в поперечних перетинах разом з изгибающим моментом Мі виникають і поперечні сили Q. Поперечний вигин зустрічається в реальних умовах навантаження частіше чистого вигину.
Якщо площину дії згинального моменту Мі проходить через центр мас поперечного перерізу, тобто через будь-яку центральну вісь перетину, вигин називають простим або плоским. в іншому випадку вигин називають косим. При плоскому вигині поздовжня вісь стрижня і після деформації залишається в площині зовнішніх сил, тобто представляє плоску криву лінію. При косому вигині площину деформації не збігається з площиною зовнішніх сил. Косий вигин відноситься до виду деформацій, які називаються складною деформацією. Визначення опорних реакцій, що згинаються стрижнів
Внутрішні сили в поперечних перетинах згинальних стрижнів визначають за допомогою методу перетинів. Використання рівнянь рівноваги і можливо для систем сил, що діють на вільні тіла. Стрижні, що піддаються деформації вигину, в реальних умовах обов'язково мають ті чи інші опори, при відсутності яких вигин стержня був би неможливий. Наявність опор (зв'язків) обмежує рух згинаного стержня і унеможливлює використання рівнянь рівноваги для визначення внутрішніх сил.
Формально невільні згинаються стрижні можна вважати вільними використовуючи принцип освобождаемості від зв'язків. Згідно з ним, будь-невільне тіло можна уявити вільним, відкинувши обмежують його рух зв'язку (опори) і замінивши їх дію силами реакції цих зв'язків. Рівняння рівноваги і можна використовувати для визначення внутрішніх сил в поперечних перетинах згинальних стрижнів за умови, що крім зовнішніх сил будуть враховуватися і сили реакцій опор. Тому перш ніж визначити внутрішні сили в поперечних перетинах згинальних стрижнів, потрібно вміти знаходити величину і напрямок реакцій опор. Відомо, що реакція зв'язку (опори) спрямована завжди в сторону, протилежну тій, куди зв'язок не дає переміщатися тілу. Якщо зв'язок перешкоджає поступальному руху тіла, її реакція - сила; якщо зв'язок перешкоджає обертального руху, її реакція - момент сил.
Розрізняють три основних типи опор стрижнів при згині.
Рухома шарнірна опора (рис. 2, а) не перешкоджає обертанню стрижня і його переміщенню уздовж опорної поверхні. Реакція опори проходить через центр шарніра і спрямована перпендикулярно опорної площини.
Нерухома шарнірна опора (рис. 2, б) допускає обертання стержня і перешкоджає його поступальному переміщенню в будь-якому напрямку. Реакція проходить через центр шарніра і може мати різне спрямування в залежності від дії системи зовнішніх сил. Розкладемо її на складові в площині зовнішніх сил, спрямовані вздовж і перпендикулярно поздовжньої осі стержня.
Жорстка закладення або защемлення (рис. 2, в) не допускає ні лінійних, ні кутових переміщень згинаного стрижня. Повна реакція опори складається з сили, яку розкладаємо на дві складові, спрямовані вздовж і перпендикулярно поздовжньої осі стержня і моменту сил (реактивного моменту), що становлять реакції опори включені в точці защемлення стрижня. Стрижень, затиснений одним кінцем і не має інших опор, називають консоллю. Консоллю називають і виступаючі за шарнірні опори частини стержня.
Далі, «замінивши» опори силами їх реакцій, складають рівняння рівноваги для системи сил, що діє на згинається стрижень. Незалежних рівнянь рівноваги для плоскої системи сил три. Завдання статично визначна, якщо число невідомих складових реакцій опор не більше трьох.
Це можливо при наступних варіантах кріплення згинаються стрижнів: защемлення стрижня одним кінцем (контактні пружини) або кріплення стрижня за допомогою рухомої і нерухомої шарнірних опор (вали). При більшій кількості невідомих складових реакцій застосовують інші, не аналізовані в посібнику, способи вирішення.
Якщо при обчисленні величину реакції опори отримали негативної. зі знаком мінус, то дійсне напрямок реакції буде протилежно прийнятому. що обов'язково потрібно враховувати при визначенні внутрішніх сил.
Визначимо реакції в опорах А і В, що згинається стрижня, схема навантаження (F, Me) і розміри (a, b, # 8467;) якого представлені на рис. 1, а. Замінимо рухому опору У реакцією RB. а нерухому шарнірну опору А - складовими RAX і RAY. «Вільний» стрижень під дією зовнішніх сил і сил реакцій опор знаходиться в спокої. Відсутність можливих складових плоского руху (поступальні переміщення уздовж осей x і y і обертальний рух в площині дії сил, тобто навколо осі z) стержня висловимо за допомогою рівнянь рівноваги:
Для діючої системи сил перше з рівнянь (1) набуде вигляду RAX = 0; друге: RB - F - RAY = 0 і третє: RB # 8467; - F # 903; a - Me = 0. З останнього рівняння визначимо, що RB = (F # 903; a + Me) / # 8467 ;. Далі, підставимо величину RB в друге рівняння, визначимо, що RAY = F - RB = F - (F # 903; a + Me) / # 8467 ;.
Визначення внутрішніх зусиль при вигині. Побудова епюр поперечних сил і згинальних моментів
При плоскому поперечному вигині в поперечних перетинах стрижня виникають наступні складові внутрішніх сил - поперечна сила Q і згинальний момент Мі. Для їх визначення використовують метод перетинів.
Поперечна сила спрямована вздовж площини перетину і її дія пов'язана з дією дотичних напружень, тобто # 964; = F (Q). Поперечна сила в будь-якому поперечному перерізі стержня чисельно дорівнює алгебраїчній сумі проекцій на площину перетину всіх зовнішніх сил і реакцій опор, що діють по одну сторону від перетину. У перетині її вважають позитивною (рис. 3, а), якщо рівнодіюча сил, що діють зліва від перетину, спрямована вгору, або рівнодіюча сил, що діють праворуч від перетину - вниз; і негативною (рис. 3, б) - при протилежному напрямку равнодействующих.
Згинальний момент діє в площині, перпендикулярній поперечним перерізом. Його дія пов'язують з дією нормальних напружень, тобто # 963; = F (Мі). Згинальний момент в будь-якому поперечному перерізі стержня чисельно дорівнює алгебраїчній сумі моментів відносно центру мас перетину зовнішніх сил і реакцій опор, що діють по одну сторону від перетину. Згинальний момент вважається позитивним, якщо стрижень в перерізі (рис. 3, в) згинається опуклістю вниз, і негативним (рис. 3, г), якщо стрижень в перерізі згинається опуклістю вгору. Знак згинального моменту в перерізі можна визначити, закріпивши умовно перетин і розглядаючи дію сил, розташованих по будь-яку сторону від нього. Наприклад, див. Рис. 1, а. сили, що діють зліва від перетину 1-1 і праворуч від перетину 2-2 згинають стрижень в цих перетинах опуклістю вниз, тобто Ми 1-1> 0 і Мі 2-2> 0.
При визначенні Q і Мі використовується змінна система координат, коли відлік перетинів ведуть або від крайнього лівого, або від крайнього правого перетину стрижня.
Для консольних жорстко закріплених з одного боку (рис. 5.24, а) стрижнів поперечну силу і згинальний момент зручніше визначити без знаходження реакцій опори, розглядаючи по відношенню до перетину сили, що діють на незакріплений ділянку стрижня. Значення Q і Мі в точці закріплення В дорівнюватимуть складовим реакції опори, тобто QB = F = RBY. МіB = F # 903; # 8467; = MRB.
Поперечна сила Q і згинальний момент Мі в загальному випадку залежать від положення перетину по довжині стрижня, тобто від величини х. Перевірку умов міцності проводять в небезпечних найбільш навантажених перетинах, в перетинах з найбільшими внутрішніми силами і максимальними напруженнями. Для знаходження небезпечних перетинів і для наочного уявлення про характер зміни внутрішніх сил будують графіки розподілу поперечних сил Q = Q (x) і згинального моменту Мі = Мі (х) по довжині стрижня, тобто епюри поперечних сил і згинальних моментів.
Стрижень розбивають на ділянки, на протязі яких навантаження однорідна. Для епюр Q і Мі проводять лінії, паралельні поздовжній осі стержня. Межі ділянок зносять на ці лінії. Для кожної ділянки становлять загальні вирази величини поперечної сили Q = Q (x) і згинального моменту Мі = Мі (х), для чого розглядають довільні перетину в межах ділянки. Далі будують епюри Q і Мі. задаючи аргументу х значення в межах кожної ділянки. Величини поперечної сили і згинального моменту відкладають як ординати епюри в масштабі: Розглянемо зміна # 964; для стержня прямокутного перерізу (рис. 5.23, б). Статичний момент заштрихованої майданчика відносно нейтральної осі z дорівнює
- відстань від осі z до центру мас відсіченої частини перерізу. Це рівняння параболи. Дотичні напруження визначимо за формулою враховуючи, що Iz = bh 3/12;
.
Найбільші дотичні напруження в поперечному перерізі діють на рівні нейтральної осі. Для стрижнів прямокутного перерізу вони в 1,5 рази більше тієї напруги, яка вийшло б при рівномірному розподілі дотичних напружень по перерізу.
Дотичні напруження при згині максимальні на нейтральній осі і при інших формах поперечного перерізу. Для стрижнів круглого поперечного перерізу вони рівні # 964; max = (4/3) (Q / A), для стрижнів кільцевого перерізу - # 964; max = 2 (Q / A).
Умова міцності стрижнів при згині по дотичним напруженням має вигляд # 964; max ≤ # 964; adm. де # 964; adm - допустиме напруження матеріалу стержня на зріз або зрушення. Відзначимо, що дотичні напруження в поперечних перетинах згинальних стрижнів багато менше нормальних, тому розрахунок на міцність ведуть зазвичай по нормальним напруженням відповідно до вираження без урахування впливу поперечних сил.
Визначення деформацій при вигині
При вигині деформація в поперечному перерізі стержня (рис. 4, а) визначається переміщенням у центру мас перетину в напрямку, перпендикулярному початкового стану осі стрижня, званим прогином і кутом повороту # 952; перетину по відношенню до свого початкового стану. Для знаходження деформацій у всіх поперечних перетинах по довжині стержня необхідно отримати залежності у = y (x) і # 952; = # 952; (x). Першу називають рівнянням вигнутої осі або рівнянням прогинів.
Дотична до вигнутої осі стрижня в будь-який її точці складе з первісної віссю кут, рівний куту повороту # 952; перетину в даній точці. тангенс кута # 952; нахилу дотичній tg # 952; = Dy / dx. Але так як фактичні значення кутів повороту поперечних перерізів при згині малі, порядку тисячних часток радіана, можна тангенс кута прирівняти значенням кута (tg # 952; ≈ # 952;) і знайти зв'язок між кутом повороту перетину і прогином у вигляді залежності # 952; ≈ ≈ dy / dx.
З курсу математики відома наступна залежність для кривизни K лінії, розташованої у площині x0y:
Але так як (dy / dx) 2 = tg 2 # 952; = # 952; 2 <<1, то выражение (2) упростим, представив в виде
Використовуючи залежність (5.67), зв'яжемо кривизну осі стержня з изгибающим моментом Мі і жорсткістю поперечного перерізу EIz:
Порівнюючи отримані вирази кривизни в залежності (3) і (4), отримаємо диференціальне рівняння зігнутої осі стержня:
інтегрування якого не становить труднощів. Вибір знака в вираженні визначається прийнятою системою координат.
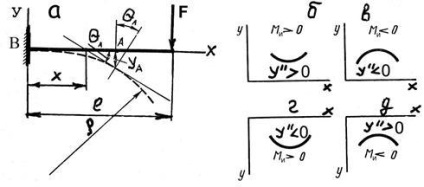
Прийнятий раніше знак згинального моменту Мі (рис. 4, б, в, г, д) не залежить від напрямку координатних осей.
Кривизна лінії позитивна, тобто y '' = d 2 y / dx 2> 0, якщо увігнутість кривої збігається з позитивним напрямком осі у (рис. 4, б, д) і навпаки (рис. 4, в, г).
При прийнятому напрямку осі у вгору, знаки правої і лівої частин рівняння (5) завжди однакові, тобто при y ''> 0 і Мі> 0, а при y '' <0 и Ми <0. Поэтому выражение 5) представим как
Для знаходження рівнянь, що визначають деформації перетинів стрижня або їх кутові і лінійні переміщення, необхідно провести інтегрування рівняння. Проинтегрировав рівняння один раз, отримаємо рівняння кутів повороту
Інтегруючи рівняння (5.80) вдруге, отримаємо рівняння прогинів
де С і D - постійні інтегрування, які визначаються з граничних умов, якими є умови кріплення згинаються стрижнів.
Так, для стержня, жорстко закріпленого одним кінцем, в місці кріплення повинні бути рівні нулю і прогин у, і кут повороту перерізу. Для стрижня, що спирається на шарнірні кріплення, прогин дорівнює нулю в місцях кріплення.
Визначити прогин і кут повороту вільного кінця консолі стержня (рис 4, а) довжиною # 8467 ;. навантаженого на кінці зосередженою силою F. Жорсткість стрижня постійна по довжині і дорівнює EI.
Початок координат приймемо в точці В жорсткого закріплення стержня. Ось у направимо вгору, вісь х - вправо.
У довільному поперечному перерізі, віддаленому на відстані х від початку координат, що вигинає момент дорівнює Мі = -F (# 8467; - x). Диференціальне рівняння зігнутої осі набуде вигляду EI (d 2 y / dx 2) = -F (# 8467; - x). Інтегруючи це рівняння, отримаємо EI (dy / dx) = = -F × [# 8467; x - (x 2/2)] + С. Інтегруючи далі, одержимо рівняння прогинів
EIy = -F [(# 8467; x 2/2) - (x 3/6)] + Cx + D.
Взявши до уваги, що в місці закріплення при х = 0 прогин у і кут повороту перетину # 952; = Dy / dx дорівнюють нулю, знайдемо, що постійні інтегрування С = 0 і D = 0. Тоді на вільному кінці стержня при х = # 8467 ;, прогин y = (-F # 8467; 3) / (3EI) і кут повороту торцевого перетину # 952; = Dy / dx = (-F # 8467; 2) / (2EI).
Знак мінус у виразах прогину і кута повороту вказує, що прогин здійснюється в напрямку, протилежному позитивного напрямку осі у. тобто вниз, а торцеве перетин повертається у напрямку руху годинникової стрілки.