Функції: \ (f \), \ (u \), \ (v \)
Аргумент (незалежна змінна): \ (x \)
Похідна функції: \ (y '\ left (x \ right) \), \ (f' \ left (x \ right) \)
Константа: \ (C \)
Дійсні числа: \ (A \), \ (\ alpha \)
Приріст функції: \ (\ Delta y \)
Приріст незалежної змінної: \ (\ Delta x \)
Диференціал функції: \ (dy \)
Диференціал незалежної змінної: \ (dx \)
Розглянемо функцію \ (y = f \ left (x \ right) \) і припустимо, що в деякій точці \ (x \) аргумент бере зріст \ (dx \), яке називається диференціалом незалежної змінної. Функція \ (y = f \ left (x \ right) \) має диференціал в точці \ (x \), якщо її приріст можна представити у вигляді суми двох доданків:
\ (\ Delta y = f \ left (\ right) - f \ left (x \ right) = A \ Delta x + \ alpha, \)
де коефіцієнт \ (A \) не залежить від \ (\ Delta x \), а величина \ (\ alpha \) має більш високий порядок малості щодо збільшення \ (\ Delta x \), тобто \ (\ alpha / \ Delta x \ to 0 \) при \ (\ Delta x \ to 0 \).
У записаної формулою головна лінійна частина приросту називається диференціалом функції \ (f \ left (x \ right) \) в точці \ (x \) і позначається у вигляді \ (dy = A \ Delta x \). У цьому виразі коефіцієнт \ (A \) дорівнює значенню похідної \ (f '\ left (x \ right) \) в точці \ (x \).
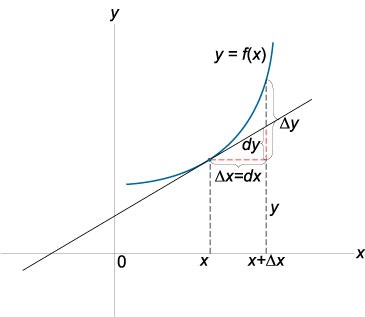
Диференціал незалежної змінної дорівнює її приросту:
\ (Dx = \ Delta x \)
Диференціал функції дорівнює добутку похідної на диференціал незалежної змінної:
\ (Dy = df \ left (x \ right) = f '\ left (x \ right) dx \)
Вираз похідною через диференціали
\ (F '\ left (x \ right) = \ large \ frac >> \ normalsize \)
Диференціал постійного числа дорівнює нулю:
\ (DC = 0 \)
Диференціал суми функцій дорівнює сумі диференціалів:
\ (D \ left (\ right) = du + dv \)
Диференціал різниці функцій дорівнює різниці диференціалів:
\ (D \ left (\ right) = du - dv \)
Постійний множник можна виносити за знак диференціала:
\ (D \ left (\ right) = Cdu \)
Диференціал твори функцій
\ (D \ left (\ right) = vdu + udv \)