Матриця перетворення координат
Візьмемо в просторі E n два різних базису e 1, e 2 e n і E 1, E 2 E n
Міркування проведемо для випадку n = 3. Один і той же вектор x щодо різних базисів має різні координати. Чи можемо написати:
Будь-вектор другого базису можемо розкласти по першому базису, тобто
В силу єдиності розкладання по даному базису ми повинні прирівняти коефіцієнти при векторах e 1, e 2, e 3 і отримані. тоді
Введемо в розгляд матриці
Тоді отримані співвідношення можна записати в матричному вигляді X = Z ⋅ X '.
Матриця Z називається матрицею перетворення координат при переході від старого базису до нового, тобто від базису e 1, e 2 e n до базису E 1, E 2 E n. Причому, стовпцями матриці перетворення координат є координати вектора нового базису E 1, E 2 E n щодо старого базису e 1, e 2 e n.
Зміна матриці лінійного оператора при переході до нового базису
Нехай в просторі E n визначено лінійний оператор A. тобто y = A ⋅ x
Або Y = A⋅X. де X (x 1, x 2. x n) T і Y (y 1, y 2. y n) T матриці-стовпці, зі ставлені з координат векторів x і y щодо даного базису n 1, e 2 e n. A - матриця лінійного оператора A.
Виберемо в тому ж просторі E n інший базис E 1, E 2 E n. Щодо нового базису матриця лінійного оператора A буде інший. Позначимо через T матрицю Перетворюва ня координат, а через X 'і Y' - одностолбцовие матриці, складені з координат векторів x і y щодо нового базису, тобто
Підставами отримане в загальний вигляд, тоді отримаємо: T ⋅ Y '= A ⋅ T ⋅ X'
Помноживши ліву і праву частини рівності зліва на T -1. отримаємо: Y '= T -1 ⋅ A ⋅ T ⋅ X'.
Отже, якщо в E n перейти до нового базису, то матриця лінійного оператора також зміниться і в найзагальнішому випадку буде дорівнює T -1 ⋅ A ⋅ T.
Приклад. Оператор A в базисі простору E 3
Знайти його матрицю в базисі
Рішення: Матриця оператора в новому базисі знаходимо за формулою B = T -1 AT. де T - матриця переходу від старого базису до нового. Матрицю переходу знаходимо за формулою T = X -1 ⋅ Y.
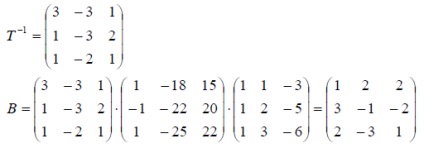
Сполучений і самосопряженних оператор
Нехай в матеріальному евклідовому просторі E n визначено лінійний оператор A
Визначення 1. Оператор A * в матеріальному евклідовому просторі E n називаючи ється зв'язаних по відношенню до лінійного оператору A в тому ж просторі, якщо його матриця в будь-якому ортонормированном базисі цього простору є транспо лося по відношенню до матриці оператора A.
Властивості сполученого оператора
1. E * = E, де E - тотожний оператор, тобто оператор, матриця якого E одинична в E n
4. якщо A -1 існує, то (A -1) * = (A *) -1.
Визначення 2. Лінійний оператор A. певний в матеріальному евклідовому просторі E n. називається самосопряженних. або симетричним. якщо він cовпа дає зі своїм зв'язаним оператором A *. тобто якщо A * = A.
Матриця самосопряженних оператора збігається з транспонованою в будь-якому ортонормированном базисі, тобто є симетричною відносно головної діагоналі.
Властивості самосопряженних оператора
1. якщо A * = A. B * = B. то (A + B) * = A * + B * = A + B;
2. якщо A - невироджених самосопряженних оператор, то (A -1) * = (A *) -1 = A -1.
Доведення . Дійсно, якщо існує A -1 і крім того A * = A. то в силу властивості 4 сполученого оператора, отримаємо (A -1) * = (A *) -1 = A -1;
3. Якщо A - самосопряженних оператор в матеріальному просторі E n. то має місце рівність:
Власні вектори і власні значення лінійного оператора
Нехай A - лінійний оператор. Нехай x∈Ε 1. де Ε 1 деякий підпростір простий ранства E n. Вектор y = A x може належати подпространству Ε 1. а може і не принади лежати.
Визначення. Підпростір Ε 1 називається інваріантним по відношенню коператоруA. якщо A x∈ Ε 1. ∀x∈ Ε 1.
Визначення. Ненульовий вектор x називається власним вектором лінійного оператора A. якщо знайдеться таке число λ. що буде виконуватися рівність A x = λ x. При цьому число λ називають власним значенням (власним числом) оператораA. відповідним вектору x. Безліч всіх власних значень оператора A називається його спектром.
Зупинимося на знаходженні власних значень і власних ВЕКТА рів лінійного оператора A. Розгляд проведемо для випадку n = 3. Отже, нехай в деякому базисі оператор A має матрицю
і нехай одностолбцовая матриця відповідає вектору x. Тоді в силу визначення
Справа звелося до вирішення системи лінійних однорідних рівнянь, записаної в матричному вигляді. Очевидно, що ця система має ненульовий розв'язок, якщо det (A - λE) = 0. Рівняння det (A - λE) = 0 називається характеристичним рівнянням оператора A; многочлен det (A - λE) називається відповідно характеристичним многочленомоператораA. У координатної формі характеристичне рівняння виглядає так:
Вирішивши його, знайдемо - власні значення лінійного оператора. Далі, для суми діагональних елементів матриці A. яку називають слідом цієї матриці trA або слідом оператор A (trA). справедлива формула. Крім того, detA = λ 1 λ 2 λ 3.
Після того як знайдені власні значення лінійного оператора A. залишається підставити їх по черзі в рівняння і знайти відповідні власні вектори x (1). x (2). x (3)
Приклад. Знайти власні значення і власні числа лінійного оператора, матриця якого
Рішення . За визначення власного вектора можемо написати - матриця - стовпець, відповід ствующая шуканого вектора x лінійного оператора A;
У матричної формі отримаємо:
Система однорідна, отже, вона має безліч рішень, якщо визначник системи дорівнює нулю, тобто маємо характеристичне рівняння:
Вирішуючи його, отримаємо такі власні значення λ 1 = -1; λ 2 = 3.
Знайдемо відповідні власні вектори.
1) λ 1 = -1 підставимо в рівняння, отримаємо
де t (1) - деякий параметр. Таким чином, маємо безліч колінеарних векторів, відповідних першому власному числу λ 1 = -1:
Цей вектор неважко пронормувати, тоді ми отримаємо одиничний власний вектор, що відповідає першому власному числу λ 1 = -1 тобто
2) λ 2 = 3 підставимо в рівняння, отримаємо
На закінчення зазначимо, що безліч всіх векторів y = A x. де x∈ E n. називається областю значень лінійного оператора A в E n. а безліч всіх векторів x∈Ε 1 ⊂ E n. таких, що A x = 0, називається ядром лінійного оператора.
Властивості власних чисел і власних векторів самосопряженних оператора
Розглянемо самосопряженних оператор A. певний в матеріальному Евкліда вом просторі E n. В силу визначення матриця його A -сімметріческая.
Теорема 1. Власні числа самосопряженних оператора A є речові числа.
Теорема 2. Власні вектори, що відповідають двом різним власним значенням самосопряженних оператора, ортогональні.
> Доказ. Нехай - різні власні значення самосопряженних оператора A. а x 1. x 2 - відповідні їм власні значення. тоді
Але тобто ліві частини рівностей рівні, отже, віднімаючи їх почленно, отримаємо: а це і означає, що власні вектори x 1. x 2 ортогональні.
Зауваження. Так як власні вектори самосопряженних оператора A ортогональні, їх можна прийняти за базис лінійного простору, в якому визначено цей лінійний оператор. Поділивши далі кожен вектор на його довжину, ми отримуємо ортонор мировалось базис.
Теорема 3. В базисі з одиничних власних векторів самосопряженних оператора матриця цього оператора діагональна, причому елементами діагоналі є її власні числа.
Доведення . Доказ проведемо для випадку n = 3. Нехай e 1. e 2. e 3 - одиничні вектори самосопряженних оператора A щодо деякого базису лінійного простору Ε 3. відповідають власним значенням цього лінійного оператора, тобто . Приймемо вектори e 1. e 2. e 3 за базис линів ного простору. Очевидно, що в цьому базисі вектори мають координати:
. Отже, матриця A оператора A в базисі e 1. e 2. e 3 має вигляд:
Вибір такого базису, в якому матриця лінійного оператора має діагональний вигляд, називається приведенням матриці до діагонального вигляду.