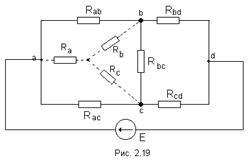
Незважаючи на те, що ця схема має одне джерело живлення, вона не піддається розрахунку методом еквівалентних опорів, так як в ній немає опорів, включених між собою послідовно або паралельно.
Особливістю цієї схеми є наявність замкнутих контурів з трьох опорів (Rab. Rbc. Rac і Rbd. Rcd. Rbc) причому точки, що розділяють кожну пару суміжних опорів, є вузловими. Такі контури називаються трикутниками опорів.
Скористаємося способом розрахунку, який складається в заміні трикутника опорів еквівалентної трипроменевою зіркою опорів (Ra. Rb. Rc) як показано на рис. пунктиром.
Заміна трикутника опорів еквівалентної зіркою, і навпаки, здійснюється за умови, що така заміна не змінює потенціалів вузлових точок a, b, c, що є вершинами трикутника і еквівалентної зірки.
Одночасно передбачається, що в іншій частині схеми, незачепленою перетворенням, режим роботи не змінюється (не змінюються струми, напруги, потужності).
Без докази наведемо формули, які служать для визначення опорів трипроменевою зірки з відомих опорам еквівалентного трикутника.
Зворотне перетворення трипроменевою зірки (Y) в еквівалентний трикутник (# 8710;), здійснюється за формулами
; .
Або через провідності
Питання для самоконтролю
· Послідовне з'єднання елементів
· Паралельне з'єднання елементів
· З'єднання елементів в U
· З'єднання елементів в D
· Взаємні преобразованіяU D
· Перетворення D U
· Перетворення паралельних гілок, що містять ЕРС
· Метод двох вузлів