Лабораторна робота № 4
ВИМІР МОМЕНТІВ ІНЕРЦІЇ ТЕЛ
Мета роботи: виміряти величину моменту інерції осесиметричних тіла (коаксіального циліндра) методом крутильних коливань, провести порівняння виміряних значень з теоретичними передбаченими значеннями моменту інерції.
Значення моменту інерції тіла відносно деякої осі (осьового моменту інерції) може бути розраховане по формулі
де - щільність тіла, а R - відстань від від елементарного обсягу dV до осі. Обчислимо за допомогою цієї формули величину моменту інерції коаксіального циліндра висотойh. мають внутрішній і зовнішній радіуси відповідно R1 і R2 щодо його осі симетрії (рис.1).
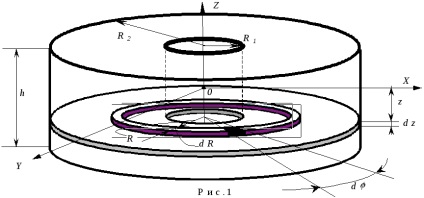
Направимо вісь Z системи координат уздовж осі симетрії циліндра, а початок системи координат (точка 0) помістимо на осі в середині висоти, тобто в центрі ваги циліндра. Розіб'ємо коаксіальний циліндр на тонкі диски висотою dz. На такому диску виділимо вузький кільцевий шар радіусом R і шириною dR. У свою чергу на цьому кільцевому шарі виділимо двома радіусами, кут між якими становить малу величину d , кільцевої сектор. Оскільки розміри цього сектора дуже малі, ми не допустимо великої помилки, якщо його обсяг dV будемо розраховувати як обсяг куба зі сторонами Rd , dR і dZ. Таким чином, елементарно малий обсяг можна представити в наступному вигляді: dV = RdRd dZ
Інтегрування по всьому об'єму циліндра еквівалентно потрійного інтегрування: по в межах від 0 до 2 , по Z - в межах від -h / 2 до h / 2. і по R в межах від R1 до R2. Таким чином, інтеграл (1) можна записати в наступному вигляді:
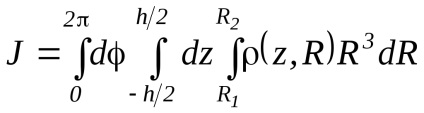
Інтегрування по дає просто множник 2 , тобто
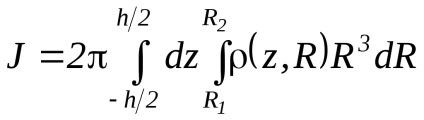
Якщо припустити, що тіло однорідне ( = Const). то після інтегрування по z і R. отримуємо
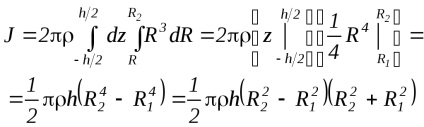
Отже, знаючи масу коаксіального циліндра, а також його внутрішній і зовнішній діаметр, можна визначити його момент інерції щодо осі симетрії.
Необхідно відзначити таку обставину. Формула (2) може бути застосована для визначення величини моменту інерції циліндра тільки в тому випадку, якщо заздалегідь відомо, що циліндр однорідний. Таке припущення (про однорідність) відсутня в методі крутильних коливань.
2. Розрахунок інтеграла у формулі (1) досить простий для тіл, що володіють деякою симетрією. Для тел довільної форми подібне інтегрування в загальному випадку неможливо. У цій ситуації для визначення моменту інерції можна скористатися наглядом якого-небудь руху, одна з характеристик якого відомим чином залежить від моменту інерції. У даній роботі такою характеристикою є період крутильних коливань. Метод крутильних коливань дозволяє визначати значення моментів інерції для тел довільної форми, що мають довільний розподіл щільності за обсягом.
Крутильними коливаннями називають коливання, які здійснює тіло, прикріплене до стрижня (або нитки), якщо стрижень (або нитка) піддати деформації кручення. Відомо, що коли коливання здійснює тіло, підвішене до пружини, схильною до деформації стиснення (розтягування), то тіло в цьому випадку рухається поступально. Якщо деформації малі, тобто справедливий закон Гука, то період таких коливань Т визначається за формулою
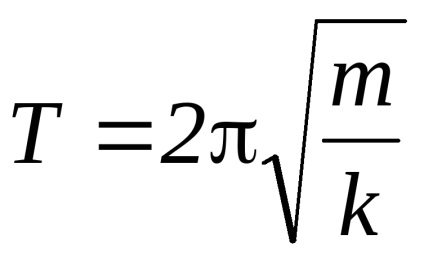
При крутильних коливаннях тіло як би робить незавершені обертання щодо деякої осі. Тому в формулу для періоду коливань замість маси входить момент інерції щодо осі обертання, а замість жорсткості k -жесткость по відношенню до деформації кручення . Таким чином, формула для періоду крутильних коливань набуває вигляду
Зв'язок між періодом коливань і моментом інерції, що задається формулою (3), дозволяє в принципі визначити величину J з вимірів періоду Т. якщо відомо значення . Однак значення зазвичай відомо з невисокою точністю, тому спосіб вимірювання J. заснований на співвідношенні (3) має велику систематичну похибку.
Систематичну похибку вимірювань, зумовлену похибкою , можна виключити, якщо метод крутильних коливань використовувати для визначення відносини моментів інерції тіл прикріплених до однієї і тієї ж нитки. Очевидно, що це відношення не залежить від величини . Насправді, нехай до нитки прикріплено деякий тіло, що має момент інерції щодо осі, що збігається з віссю обертання, рівній J0. Період коливань Т 0 такого тіла дорівнює
Якщо до першого тіла прикріпити інше тіло, момент інерції якого щодо осі обертання дорівнює J. то момент інерції такої системи буде дорівнює сумі J + J0. Відповідно зміниться і період коливань такої системи.
Розділивши (5) на (4), знайдемо
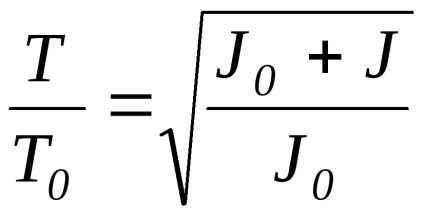
З формули (6) видно, що систематична похибка визначення відносини J / J0 залежить тільки від систематичних похибок вимірювання періодів коливань Т і Т0. які у сучасних секундомірів малі. Очевидно, що якщо величина J0 щодо осі обертання відома з яких-небудь інших міркувань, то, обчисливши співвідношення J / J0 за формулою (6), легко визначити момент інерції J щодо тієї ж осі обертання.
Установка для вимірювання моменту інерції методом крутильних коливань є, зібрані на масивному підставі колонку для кріплення досліджуваних зразків і секундомір. На колонці за допомогою притискних гвинтів розміщуються три кронштейна. Верхній і нижній кронштейни мають затискачі, Службовці для закріплення сталевого дроту, до якої підвішується рамка з платформою у вигляді тонкого диска. Момент інерції рамки з платформою J0 щодо осі обертання відомий. Його значення наведено на установці. Конструкція рамки така, що дозволяє розміщувати на платформі різні тіла, момент інерції яких необхідно виміряти. На середньому кронштейні закріплена сталева плита, яка служить підставою фотоелектричному датчику, електромагніту і кутовий шкалою. Електромагніт може змінювати положення на плиті, а його положення щодо фотодатчика показує на кутовий шкалою стрілка, прикріплена до електромагніту.
На лицьовій панелі миллисекундомером знаходяться:
- клавіша "Мережа" - вмикач мережі. Натискання цієї клавіші викликає включення напруги живлення. При цьому на двох цифрових табло повинні висвітлюватися нулі, а також повинна горіти лампочка фотодатчика;
- клавіша "Скидання" - скидання секундоміра. Натискання цієї клавіші викликає скидання схем блоку вимірів і генерування сигналу, який дозволить вимір;
- клавіша "Стоп" - закінчення вимірювань. При натисканні цієї кнопки генерується сигнал на закінчення відліку часу;
- клавіша "Пуск" - управління електромагнітом. Натискання цієї клавіші викликає відключення струму, що живить електромагніт.
На лицьовій панелі знаходиться також два цифрових табло. На одному висвічується число періодів коливань рамки, на іншому - час, протягом якого ці коливання відбуваються.
При натисканні клавіші "Мережа" секундомір встановлюється в початковий стан (нулі на цифрових індикаторах) і блокується схема формування імпульсів. Це блокування знімається сигналом, який виробляється при натисканні клавіші "Скидання". Натискання клавіші "Пуск" звільняє електромагніт, і починаються крутильні коливання маятника. У момент першого переривання світлового потоку, що падає на фототранзистор від лампочки, генерується електричний імпульс, який підключає до лічильника часу кварцовий генератор. Лічильник підраховує кількість імпульсів, наступних з кварцового генератора з частотою 10 КГц. Одночасно інший лічильник підраховує кожен (наступний після першого) непарний імпульс. Проходження кожного такого непарного імпульсу відповідає одному коливанню і показання цифрового табло лічильника періодів зміниться на одиницю.
При натисканні клавіші "Стоп" формується сигнал, який готує схеми до кінця рахунку. Повністю рахунок припиняється в момент генерації чергового непарного імпульсу фотодатчиком. При цьому на цифрових табло висвічується число коливань і час, протягом якого вони здійснилися. Систематична похибка вимірювання часу становить 0,02%.
Таким чином, методика вимірювання осьового моменту інерції тіла зводиться до наступного. Спочатку слід переконатися в застосовності формули (6), тобто переконатися в тому, що коливання слабо затухаючі. Після цього визначити період коливання порожньої платформи і платформи, з встановленим на неї тілом. Потім розрахувати J зразка за формулою (6).
Описаний метод придатний для визначення моменту інерції тіла довільної форми щодо осі коливань. В окремому випадку, коли тіло встановлено на платформі так, що вісь коливань збігається з віссю симетрії тіла, то методом крутильних коливань визначається момент інерції щодо осі симетрії.
ВИКОНАННЯ РОБОТИ ТА УМОВИ ЕКСПЕРИМЕНТУ
1. Включити прилад натисканням клавіші "Мережа", переконатися в тому, що індикатори вимірювача висвічують нулі, і світяться фотодатчика. Встановити електромагніт в деякий стан і за допомогою його зафіксувати рамку з платформою.
2. Переконатися в тому, що коливання крутильного маятника є слабо затухаючими. Для цього, натиснувши послідовно клавіші "Скидання" і "Пуск", визначте число коливань N, за яке амплітуда зменшується в 2-3 рази. Якщо N> 10, то загасання мало і можна користуватися формулою (4). Вимірювання N провести для порожньої платформи і для платформи з встановленим на неї кільцем.
3. Визначити час t0. протягом якого рамка з порожньою платформою зробить N коливань. Вимірювання слід провести при різних N (всього 5-7 разів). Очевидно, що Т0 = t0 / N. Дані занести в таблицю. Розрахувати середнє значення, випадкову і систематичну похибки.
4. Помістити на платформу досліджуваний зразок. Стежити за тим, щоб центр кільця збігався з центром платформи. Виміряти період коливань Т. так само як і в пункті 3.
5. Розрахувати момент інерції кільця за формулою (6).
6. Визначити масу кільця М. Для цього зважити кільце на технічних вагах двічі, маючи в своєму розпорядженні його на різних чашках. Знайти середнє цих вимірів, розрахувати випадкову похибку, систематичну похибку зважування вважати рівною масі найменшого використовуваного Важок.
7. Виміряти внутрішній і зовнішній радіуси кільця за допомогою штангенциркуля. Вимірювання проводити не менше 5 разів. Розрахувати середнє значення R1 і R2. їх випадкові і систематичні похибки.
8. Розрахувати момент інерції кільця за формулою (2).
ОБРОБКА РЕЗУЛЬТАТІВ ЕКСПЕРИМЕНТУ
Величини моментів інерції кільця, виміряні як методом крутильних коливань, так і методом, що використовує формулу (2), є результатами непрямих вимірювань. Отримаємо формули для розрахунку похибки вимірювань величин J. отриманих цими методами. Для методу крутильних коливань, відповідно до правил розрахунку похибки непрямих вимірювань і формулою (6), отримуємо
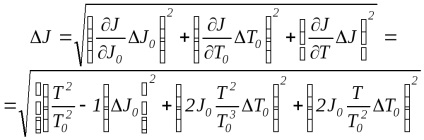
Розділивши обидві частини отриманого виразу на J. отримуємо
Підставляючи в (7) замість J0. T0 і T спочатку випадкові, а потім систематичні похибки вимірюваних прямо величин, розраховуються похибки J. обумовлені відповідно випадковими (oJ) і систематичними (cJ) похибками прямих вимірювань. Повна похибка дорівнює.
Аналогічно виводиться формула і для розрахунку похибки вимірювання методом, що використовує формулу (5)
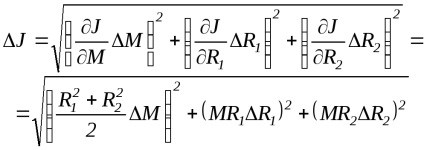
Так само, як і раніше, за формулою (8) розраховуються похибки, обумовлені випадковими і систематичними похибками прямих вимірювань, а потім і повна похибка.
Після обчислення похибок можна провести коректне порівняння результатів вимірювання величин моменту інерції, отриманих різними способами. У тому випадку, якщо результати вимірювань розрізняються на величину більшу, ніж похибки експерименту, необхідно зробити висновок про можливі причини такої розбіжності.