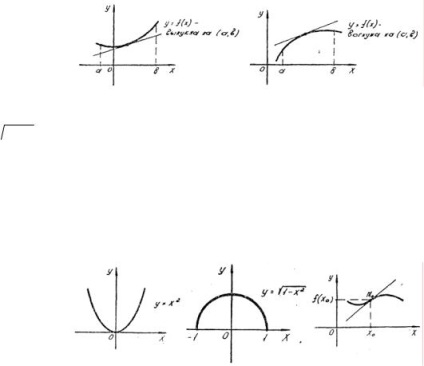
Графік функції, що диференціюється називається увігнутим в інтервалі (a, b), якщо він розташований вище будь-якої своєї дотичній в цьому інтервалі (рис. 10).
Графік функції, що диференціюється називають опуклим в інтервалі (a, b), якщо він розташований нижче будь-якої своєї дотичній в цьому інтервалі (рис. 11).
Так парабола у = х 2 - функція увігнута на всій числовій осі (рис. 12), а півколо y = 1 - x 2 (рис. 13) має опуклий графік на відрізку [- 1; 1].
Точка М 0 (x 0. f (x 0)), що лежить на графіку і відокремлює опуклу частину графіка від увігнутої, називається точкою перегину функції у = f (x) (рис. 14).
За опуклість (увігнутість) функції "відповідає" втораяпроізводная функції у = f (x).
Справедливо наступне твердження: якщо функція у = f (x) має другу похідну f '' (x) у всіх точках інтервалу (a, b) і якщо у всіх точках цього інтервалу f '' (x) <0. то график функции в интервале ( a, b ) – выпуклый, если же f ′′ ( x )> 0, то графік функції увігнутий в цьому інтервалі.
Мал. 12 Рис. 13 Рис. 14
Точки перегину слід шукати серед тих точок, в яких друга похідна
Якщо зліва від такої точки і праворуч від неї f '' (x) має різні знаки, то знайдена точка буде точкою перегину.
Побудова графіка функції значно полегшується, якщо знати його асимптоти.
Асимптотой кривої називається пряма, відстань від якої до точки, що лежить на кривій, прагне до нуля при необмеженому видаленні від початку координат цієї точки по кривій.
Асимптоти можуть бути вертикальними, похилими і горизонтальними.
Кажуть, що пряма є вертикальною асимптотой графіка функції y = f (x), якщо
Але якщо хоча б один з цих меж не існує або дорівнює нескінченності, то крива y = f (x) похилих асимптот немає.
Відзначимо, що слід окремо розглянути випадки х → + ∞ і х → - ∞. окремим випадком
похилій асимптоти при k = 0 і b = lim f (x) буде горизонтальна асимптота. Тому y = b -
рівняння горизонтальної асимптоти.
Розглянемо графік функції на рис. 15. Точки х = х 2. х = х 4 - точки екстремумів функції, точка х = х 1 - це точка перегину. Точка х = х 3 є особливою точкою для функції, в ній f (x) терпить розрив, а пряма х = х 3 є вертикальною асимптотой
графіка функції. Пряма y = kx + b теж буде асимптотой графіка, тільки похилій, пряма у = 0 - горизонтальна асимптота графіка.
Якщо точка М (х, у) лежить на графіку і необмежено віддаляється від початку координат, то вона наближається до однієї з цих прямих; відстань від точки М (х, у) до асимптот прагне до нуля.
Загальна схема дослідження функції та побудови графіка
Для загального дослідження функції та побудови графіка корисно дотримуватися наступного плану.
Знайти область визначення функції, точки розриву функції та інтервали неперервності Знайти (якщо це можливо) точки перетину графіка з осями координат.
Знайти інтервали знакопостоянства функції (проміжки, на яких f (x)> 0 або f (x) <0). Решить вопрос о чётности, нечётности, симметрии, периодичности функции.
Якщо є точки розриву 2 - го роду, знайти вертикальні асимптоти. Знайти, якщо вони є, похилі і горизонтальні асимптоти.
За допомогою 1 - ой похідної знайти точки екстремуму і області зростання та спадання даної функції. Знайти екстремальні значення функції.
За допомогою 2 - ий похідною знайти точки перегину, області опуклості і угнутості. Побудувати графік.
Приклад: Дослідити функцію y =