Додавання і віднімання алгебраїчних дробів з різними знаменниками
ДОДАВАННЯ І віднімання АЛГЕБРАЇЧНИХ ДРОБІВ з різними знаменниками
Додавання і віднімання алгебраїчних дробів з різними знаменниками виконують за тим же алгоритмом, що використовується для додавання і віднімання звичайних дробів з різними знаменниками: спочатку призводять дроби до спільного знаменника з допомогою відповідних додаткових множі-
телей, а потім складають або віднімають отримані дробу з однаковими знаменниками за правилом з § 3. Можна сформулювати алгоритм, що охоплює будь-які випадки складання (вирахування) алгебраїчних дробів.
Алгоритм складання (вирахування) алгебраїчних дробів

Приклад 1. Виконати дії:
Рішення. Для кожної пари заданих тут алгебраїчних дробів спільний знаменник був знайдений вище, в прикладі з § 2. Спираючись на вказаний приклад, отримуємо:
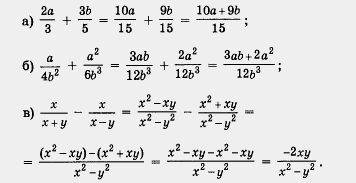
Найважче в наведеному алгоритмі - це, звичайно, перший крок: пошук спільного знаменника і приведення дробів до спільного знаменника. У прикладі 1 ви цієї проблеми, може бути, не відчули, оскільки ми скористалися готовими результатами з § 2.
Щоб виробити правило відшукання загального знаменника, проаналізуємо приклад 1.
Для дробів спільний знаменник є число 15 воно ділиться і на 3 і на 5, є їхнім спільним кратним (навіть найменшим спільним кратним).
Для дробів - спільним знаменником є одночлен 12b 3. Він ділиться і на 4b 2 і на 6b 3. т. Е. На обидва одночлена, службовці знаменниками дробів.
Зверніть увагу: число 12 - найменше спільне кратне чисел 4 і 6. Мінлива b входить в знаменник першого дробу з показником 2, в знаменник
другого дробу - з показником 3. Це найбільше значення показника 3 фігурує в загальному знаменнику.
для дробів
спільним знаменником служить твір (х + у) (х - у) - воно ділиться і на знаменник х + у і на знаменник х-у.
При знаходженні спільного знаменника доводиться, природно, всі задані знаменники розкладати на множники (якщо це не було підготовлено в умови). А далі йде провести роботу по етапах: знайти найменше спільне кратне для числових коефіцієнтів (мова йде про цілочисельних коефіцієнтах), визначити для кожного кілька разів зустрічається літерного множника найбільший показник ступеня, зібрати все це в один твір.
Тепер можна оформити відповідний алгоритм.
Алгоритм відшукання загального знаменника для декількох алгебраїчних дробів

Перш ніж рухатися далі, спробуйте застосувати цей алгоритм до обгрунтування пошуку спільного знаменника для алгебраїчних дробів з прикладу 1.
Зауваження. Насправді загальних знаменників для двох алгебраїчних дробів можна знайти скільки завгодно. Наприклад, для дробів загальним
знаменником може бути і число 30, і число 60, і навіть одночлен 15а2Ь. Справа в тому, що і 30, і 60, і 15 а 2 b можна розділити як на 3, так і на 5. Для
дробів -
спільним знаменником, крім знайденого вище одночлена 12b. може бути і 24b 3 і 48а 2 b 4. Чим же одночлен 12b 3 краще, ніж 24b 3. ніж 48а 2 b 4. Він простіше (по виду). Його іноді називають навіть не спільним знаменником, а найменшим спільним знаменником. Таким чином, наведений алгоритм - це алгоритм
відшукання самого простого із загальних знаменників декількох алгебраїчних дробів, алгоритм відшукання найменшого спільного знаменника.
Знову повернемося до прикладу 1, а. Щоб скласти алгебраїчні дроби. треба було не тільки знайти спільний знаменник (число 15), а й відшукати для кожної з дробів додаткові множники, які дозволили б привести дроби до спільного знаменника. Для дробу таким додатковим мно-
жителем служить число 5 (чисельник і знаменник цього дробу помножили додатково на 5), для дробу число 3 (чисельник і знаменник цього дробу помножили додатково на 3).
Додатковий множник є частка від ділення загального знаменника на знаменник даної дробу.
Зазвичай використовують такий запис:
Знову повернемося до прикладу 1,6. Спільним знаменником для дробів є одночлен 12b 3. Додатковий множник для першого дробу дорівнює Зb (оскільки 12b 3. 4b 2 = З Ь), для другого дробу він дорівнює 2 (оскільки 12b 3. 6b 3 = 2). Значить, рішення прикладу 1,6 можна оформити так:
Вище був сформульований алгоритм відшукання загального знаменника для декількох алгебраїчних дробів. Але досвід показує, що цей алгоритм не завжди буває зрозумілий учням, тому ми дамо кілька видозмінену формулювання.
Правило приведення алгебраїчних дробів до спільного знаменника

Приклад 2. Спростити вираз
Рішення.
Перший етап. Знайдемо загальний знаменник і додаткові множники.
маємо
4а 2 - 1 = (2а - 1) (2а + 1),
2а 2 + а = а (2а + 1).
Перший знаменник беремо цілком, а з другого - додаємо множник а, якого немає в першому знаменнику. Отримаємо спільний знаменник
Зручно розташувати записи у вигляді таблиці:
Другий етап.
Виконаємо перетворення:
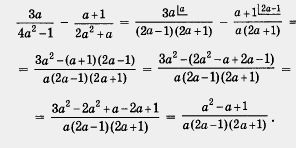
При наявності деякого досвіду перший етап можна не виділяти, виконуючи його одночасно з другим етапом.
На закінчення розглянемо більш складний приклад (для бажаючих).
Приклад 3. спростити вираз
Рішення.
Перший етап.
Розкладемо все знаменники на множники:
1) 2а 4 + 4а 3 b + 2a 2 b 2 = 2а 2 (а 2 + 2аb + b 2) = 2а 2 (а + b) 2;
2) 3ab 2 - За 3 = За (b 2 - а 2) = За (b - а) (b + а);
3) 6а 4 -6а 3 b = 6а 3 (а- b).
Перший знаменник беремо цілком, з другого візьмемо відсутні множники 3 і b - а (або a - b), з третього - відсутній множник а (оскільки третій знаменник містить множник а 3).
Зауважимо, що якщо у додаткового множника з'являється знак «-», то його зазвичай ставлять перед усією дробом, т. Е. Перед другою дробом доведеться поміняти знак.
Другий етап.
Виконаємо перетворення:
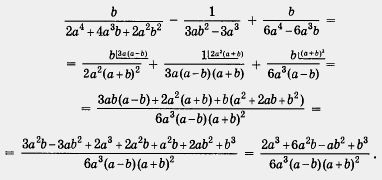
Відзначимо, що заміна вираження, даного в прикладі 3, тієї алгебраїчної дробом, яка вийшла в результаті, є тотожне перетворення при допустимих значеннях змінних. В даному випадку допустимими є будь-які значення змінних а і Ь, крім a = 0, a = b, a = - b (в цих
випадках знаменники звертаються в нуль).