Під ред. А.В. Сидоровича
Розділ I. Мікроекономіка
Глава 8. Вибір споживача і функція попиту. Індивідуальний і ринковий попит
еквімаржінальний принцип
Згадаймо, що в точці MRSx = -dX2 / dX1. При переміщенні уздовж даної кривої байдужості рівень корисності, зрозуміло, не змінюється, отже, dU = 0. Але ми знаємо, що (при стандартних припущеннях) диференціал функції двох змінних можна уявити так:
Прирівнявши цей вислів до 0 (маючи на увазі переміщення уздовж кривої байдужості), переносячи одна з складових в іншу частину і розділивши на відповідні вирази, отримуємо:
Зліва у нас вийшла гранична норма заміни в даній точці, а праворуч співвідношення граничних корисностей двох видів благ:
Звідси умова рівноваги споживача може бути виражене в такий спосіб:
Перегрупувавши члени в останній пропорції для випадку n благ, отримуємо:
Отже, в точці оптимуму споживача відношення граничних корисностей дорівнює відношенню цін споживаних благ. Ця умова вірно для завдання споживчого вибору з будь-яким числом благ. Відповідно до нього споживач розподіляє свій грошовий дохід таким чином, щоб остання грошова одиниця, витрачена на кожен товар, давала одну і ту ж граничну корисність. Якби це було не так, то споживач міг би грошову одиницю, що дає меншу граничну корисність, перерозподілити туди, де її гранична корисність була б більше. Це - так званий еквімаржінальний принцип.
У разі двох товарів споживач максимізує свою корисність, якщо одночасно виконуються дві умови. Перша умова полягає в тому, що MRS для даних товарів повинна дорівнювати відношенню їх цін. Друга умова - виділений для придбання даних товарів дохід витрачається повністю. Тоді ми отримуємо внутрішнє рішення.
У тому ж випадку, коли криві байдужості перетинаються з осями координат (в тому числі, коли розглянуті товари є абсолютними замінниками для даного споживача), гранична норма заміни в рамках укладеного між осями координат простору благ може виявитися весь час більше або весь час менше нахилу лінії бюджетного обмеження. Тоді точка дотику кривої байдужості і бюджетної лінії не може бути найкращим виходом для даного споживача. Очевидно, що в такому випадку при застосуванні послідовного перебору можливостей споживач опиниться на одній з осей координат, в точці перетину даної осі одночасно з кривою байдужості і лінією бюджетного обмеження. Подібний результат справи буде називатися кутовим рішенням проблеми вибору споживача, а оптимальний в такому випадку набір буде містити, зрозуміло, тільки один вид благ. Іншими словами, при даних перевагах і співвідношенні цін споживачеві для максимізації своєї корисності виявляється найкраще зовсім утриматися від покупки одного з благ і всі наявні ресурси направити на покупку блага іншого виду (рис. 8.2).
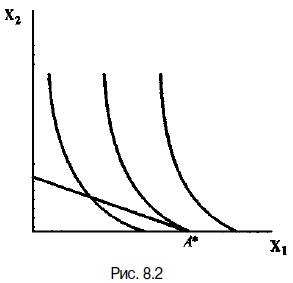
В даному випадку MRSx1x2> Р1 / Р2 і в оптимальний набір А * (Х1 *; X2 *) входить тільки певну кількість X * блага першого виду, а X * = 0.
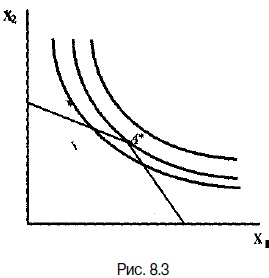
Якщо лінія бюджетного обмеження має вид ламаної, то максимум корисності споживача може досягатися в одній з точок зламу (рис. 8.3).