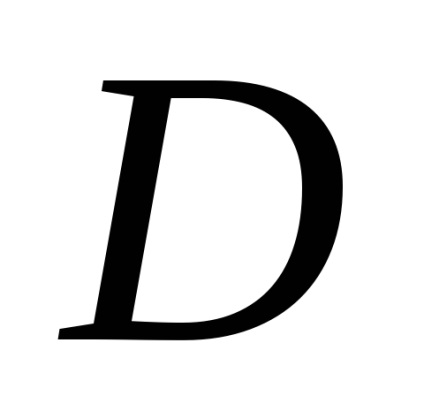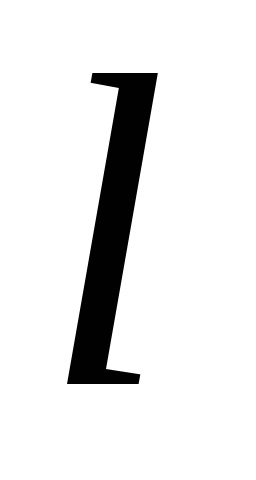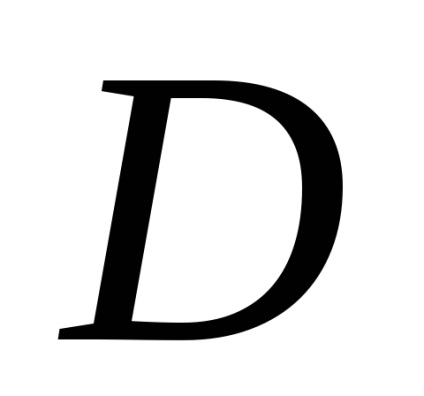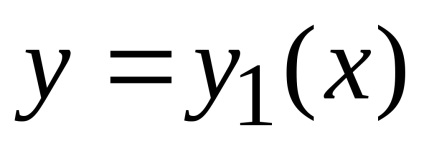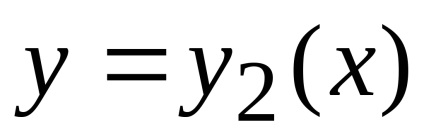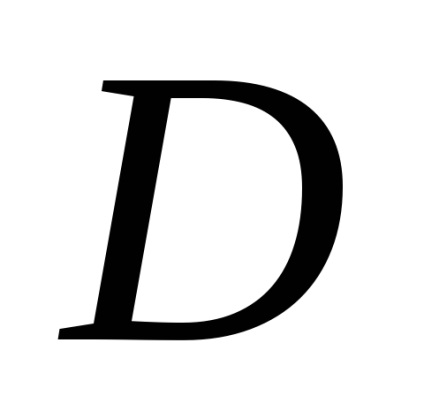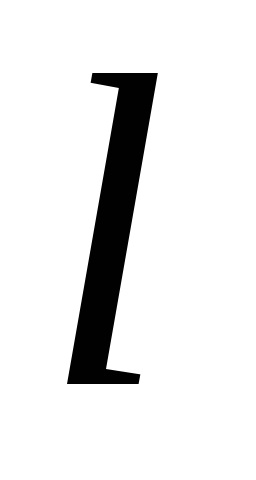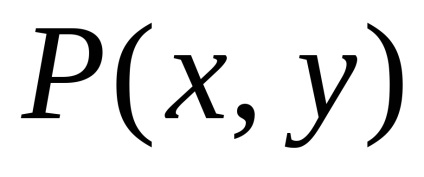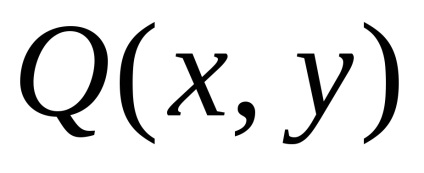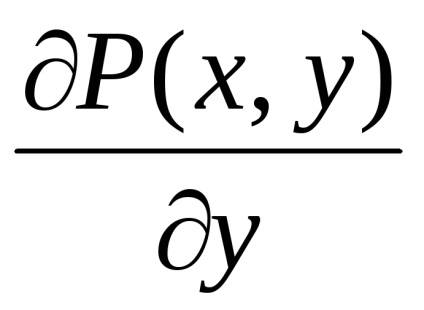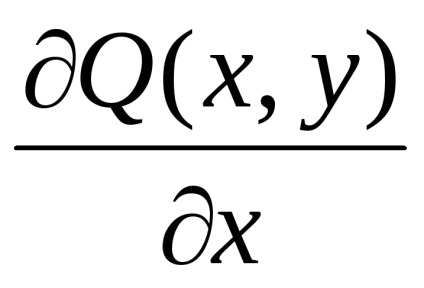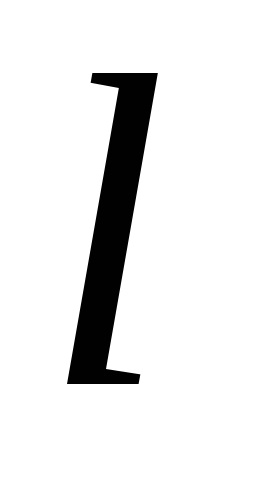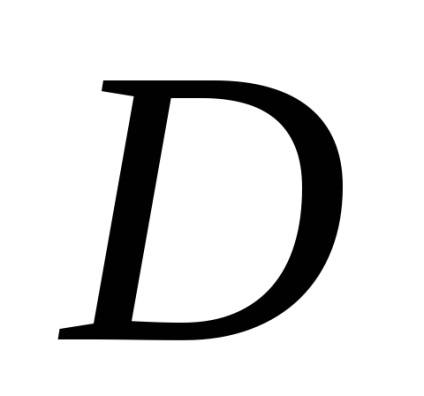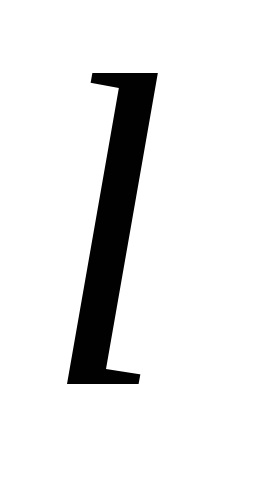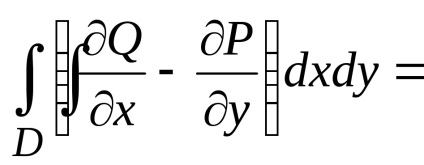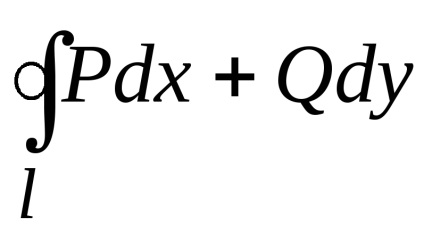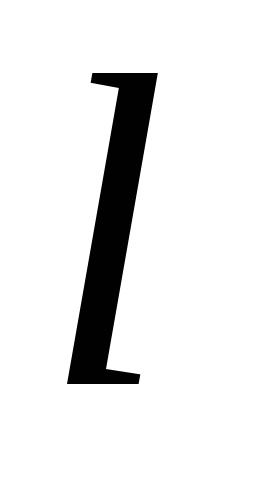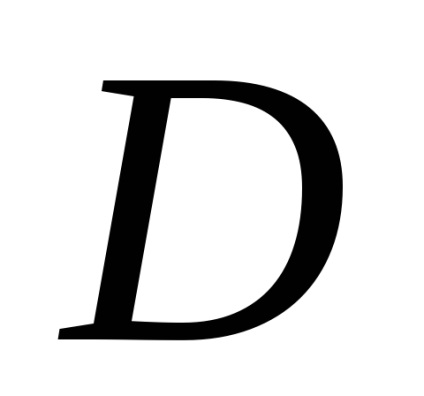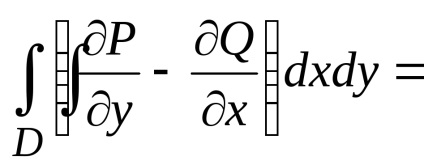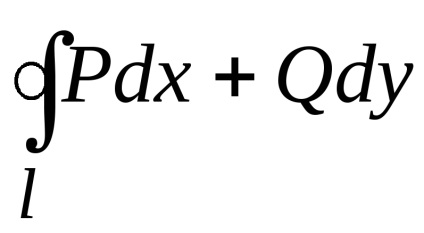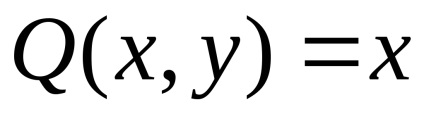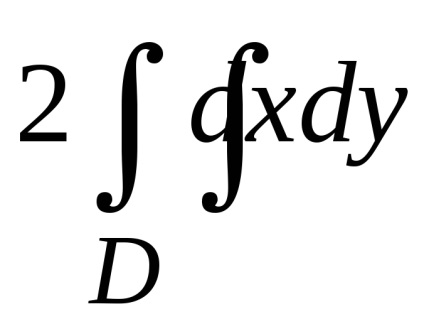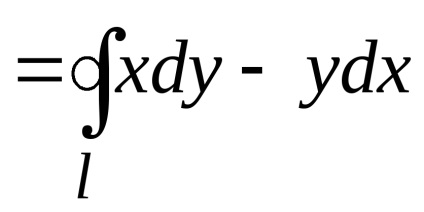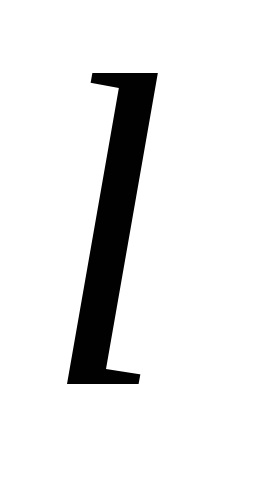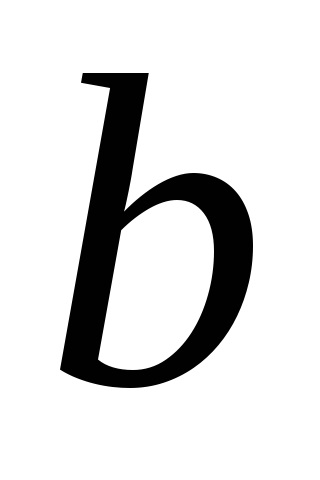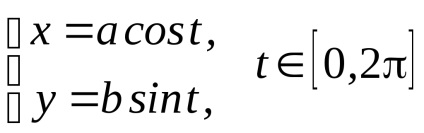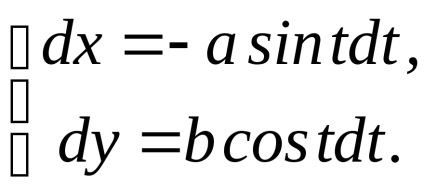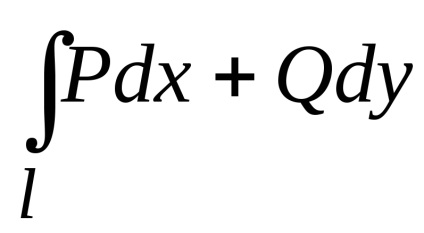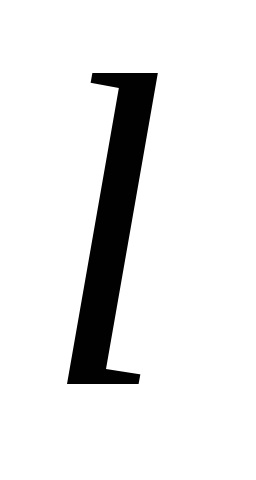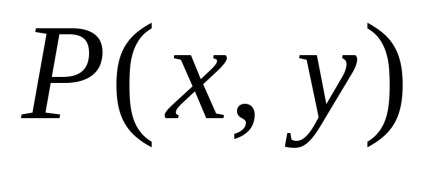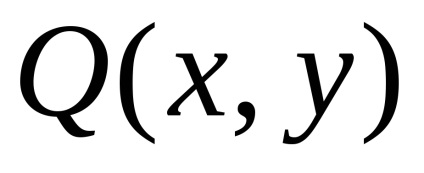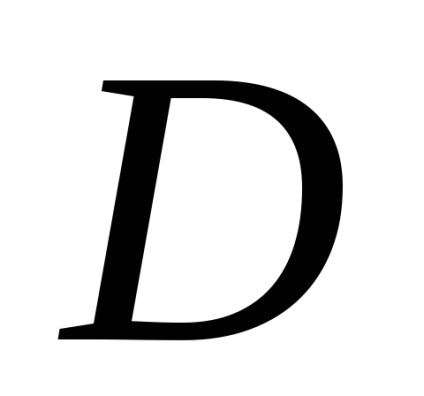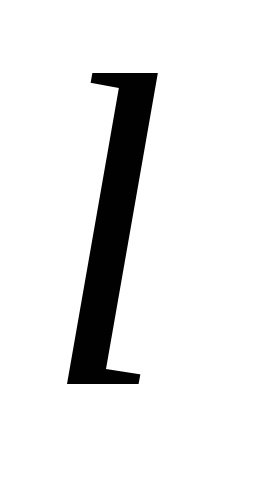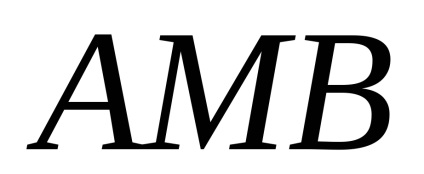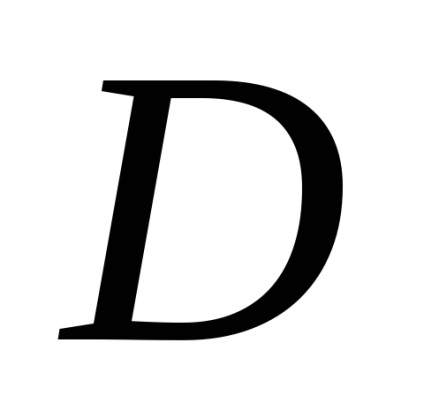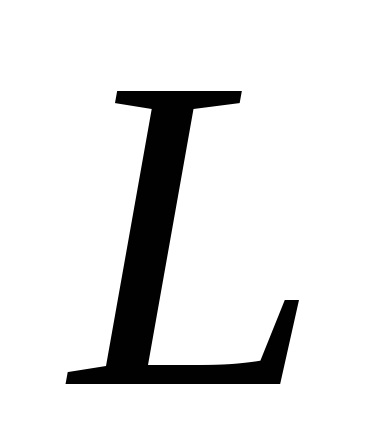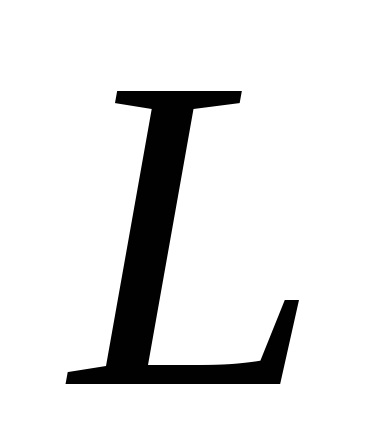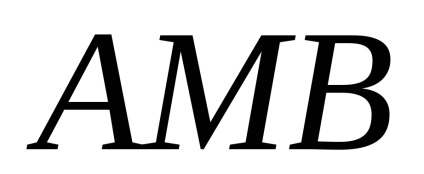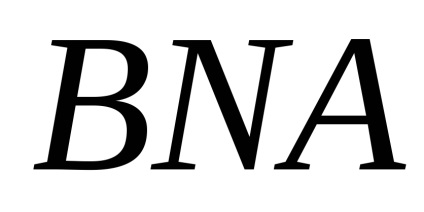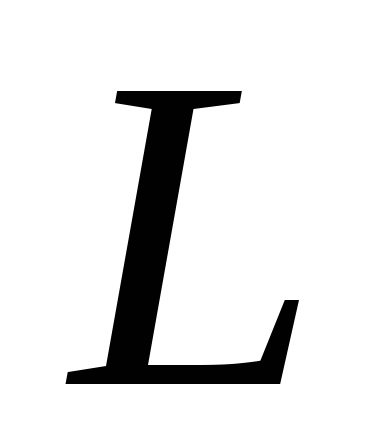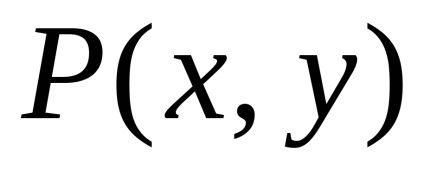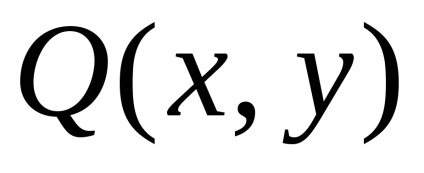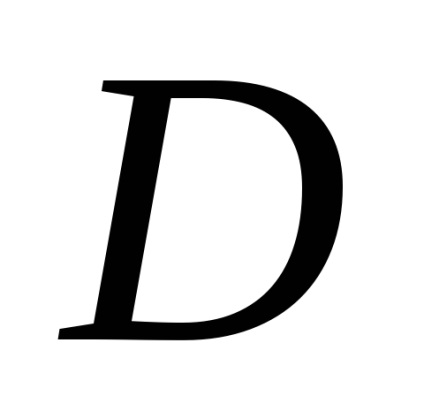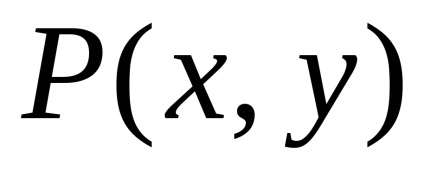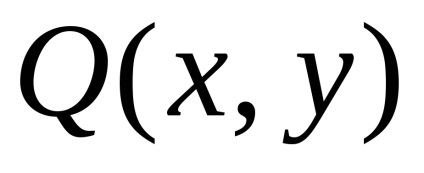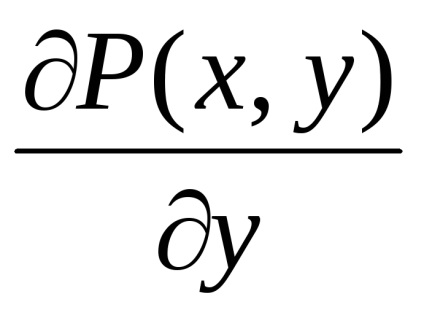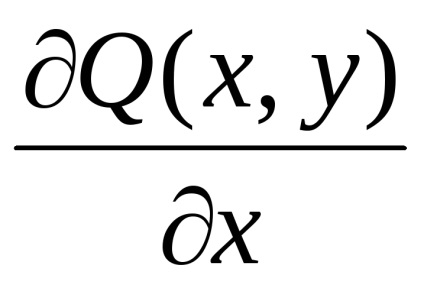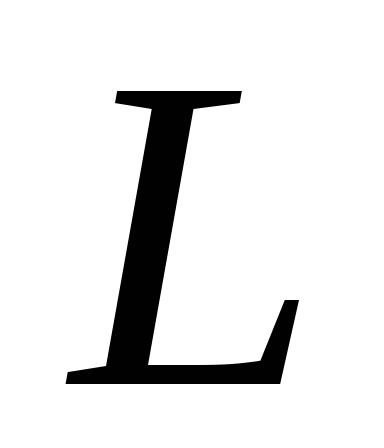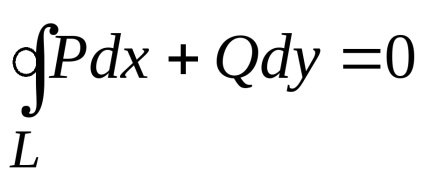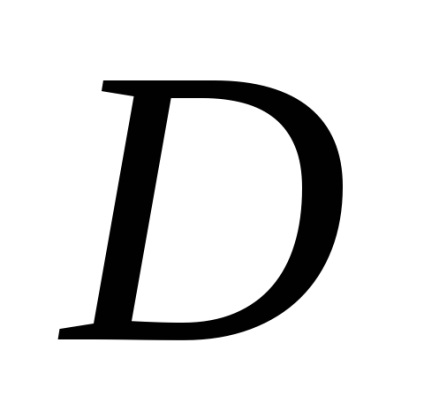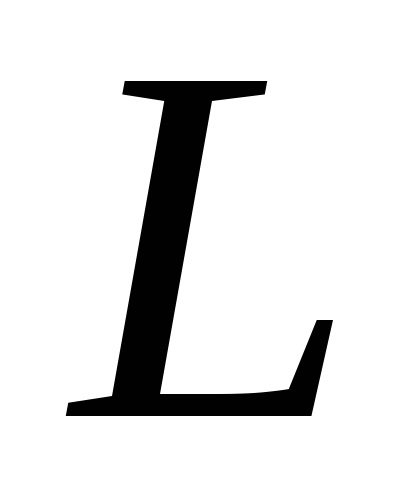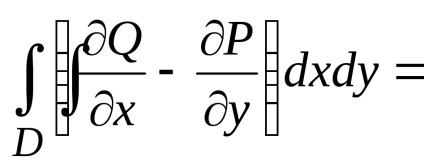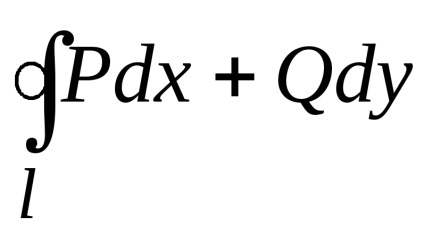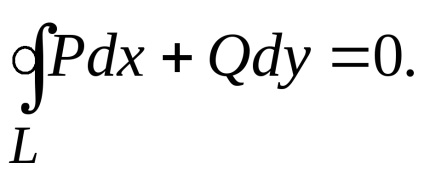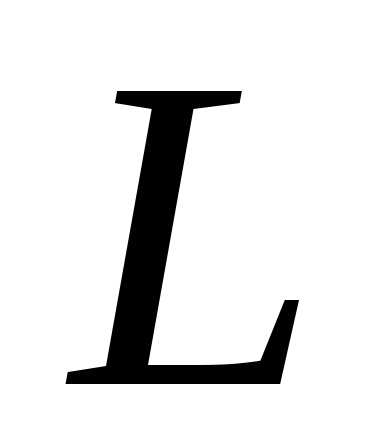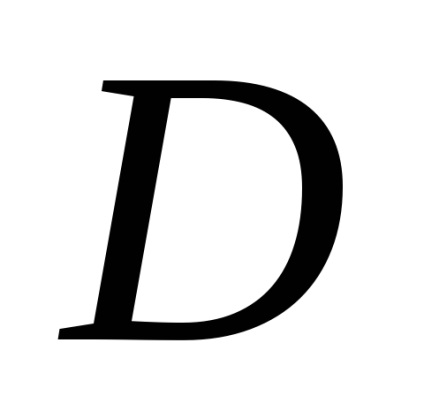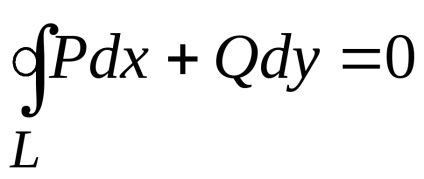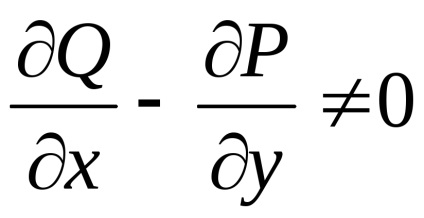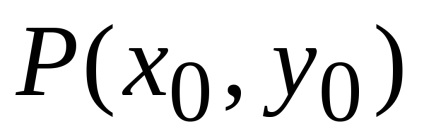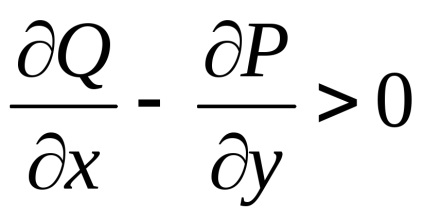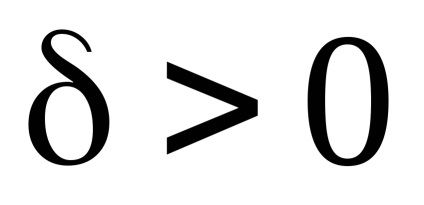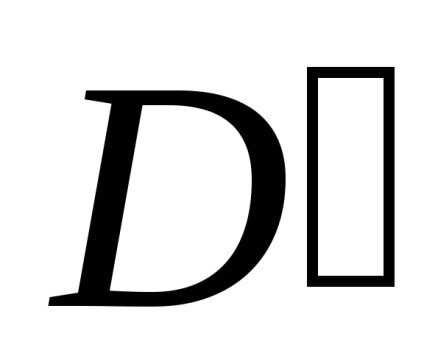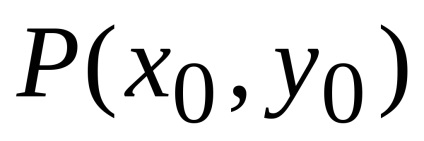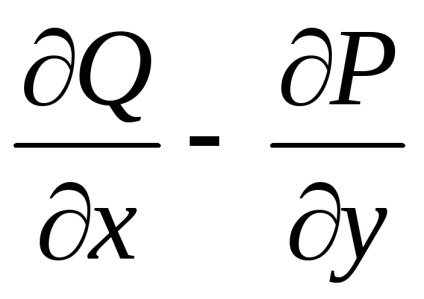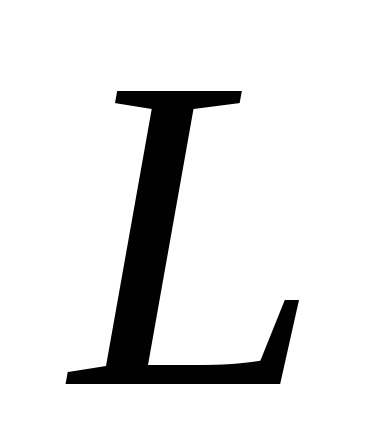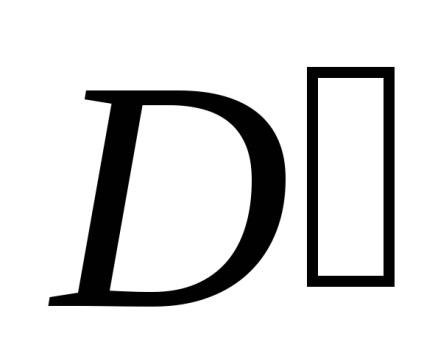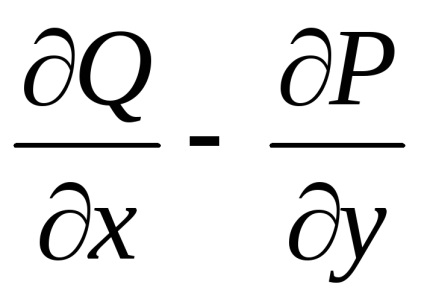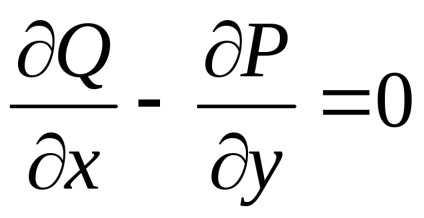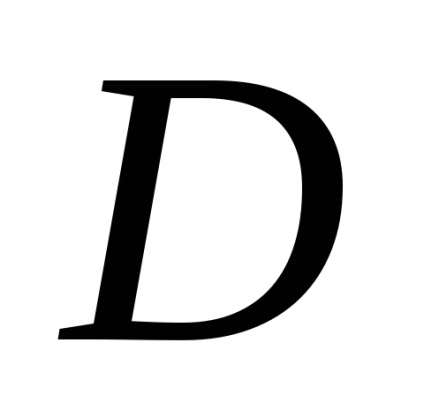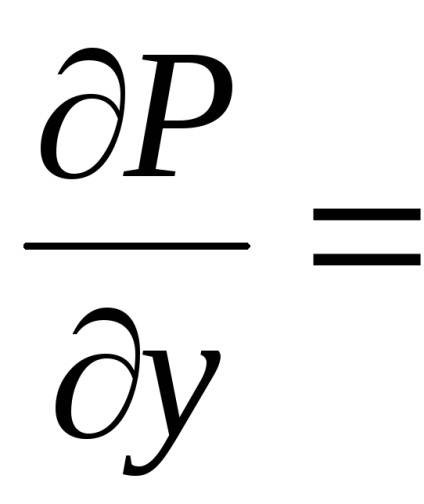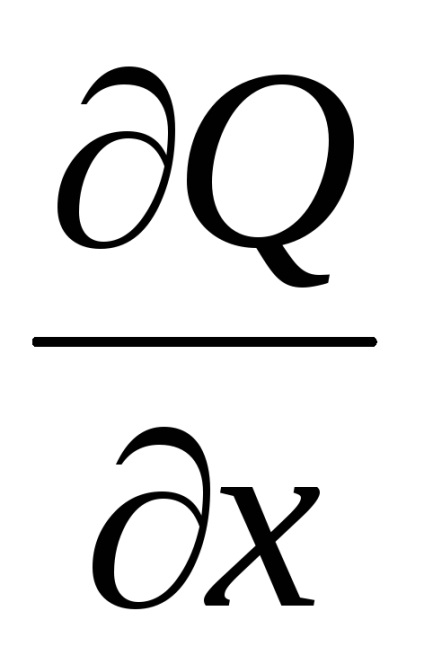Формула Гріна встановлює зв'язок між подвійним інтегралом по області
і криволінійним інтегралом по контуру
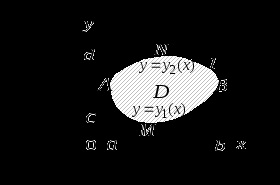
, обмежує цю область. Будемо вважати, що область
є стандартною в напрямку кожної координатної осі і знизу обмежена графіком функції
(дугою
), Зверху - графіком функції
(дугою
), Які разом складають замкнутий контур
.
Нехай в області
і на її кордоні
задані функції
і
безперервні разом зі своїми приватними похідними
,
, тоді
,
де обхід контуру
відбувається в позитивному на-правлінні, т. е. проти годинникової стрілки (область
залишається зліва). отже,
де обхід контуру
також відбувається в позитивному напрямку.
Віднімаючи почленно (1) з (2), отримуємо формулу Гріна
.
Зауваження 1. Якщо обхід контуру
відбувається в негативному напрямку, т. е. за годинниковою стрілкою (область
залишається праворуч), то формула Гріна набирає вигляду
.
Зауваження 2. Формула Гріна дає можливість обчислювати площу області за допомогою криволінійного інтеграла. Дійсно, якщо,
, то формула Гріна перепишеться так:
,
де обхід контуру
відбувається проти годинникової стрілки.
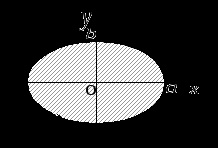
Приклад. Визначити за допомогою криволінійного інтеграла площа, обмежену еліпсом з півосями
і
.
Рішення. Запишемо параметричні рівняння еліпса
.
І за формулою (3) отримаємо
.
Умови незалежності криволінійного інтеграла від шляху інтегрування
Розглянемо криволінійний інтеграл
,
взятий за деякою плоскої кривої
, з'єднує точки
і
.
Будемо припускати, що функції
і
мають безперервні приватні похідні в даній області
. З'ясуємо, за яких умов написаний криволінійний інтеграл не залежить від форми кривої
, а залежить тільки від положення початкової і кінцевої точок
і
.
Розглянемо дві довільні криві
і
, що лежать в даній області
і що з'єднують точки
і
. нехай
.
Тоді на підставі властивостей 1 і 2 криволінійних інтегралів маємо:
,
т. е. криволінійний інтеграл по замкнутому контуру
В останній формулі криволінійний інтеграл взятий по замкнутому контуру
, складеним з кривих
і
. цей контур
можна, очевидно, вважати довільним.
Таким чином, з умови, що для будь-яких двох точок
і
криволінійний інтеграл не залежить від форми з'єднує їх кривої, а залежить тільки від положення цих точок, слід, що криволінійний інтеграл по будь-якому замкнутому контуру дорівнює нулю.
Справедливо і зворотне висновок: якщо криволінійний інтеграл по будь-якому замкнутому контуру дорівнює нулю, то цей криволінійний інтеграл не залежить від форми кривої, що з'єднує дві будь-які точки, а залежить тільки від положення цих точок. Дійсно, з рівності (2) слід рівність (1).
Природно виникає питання: яким умовам повинні задовольняти функції
і
для того, щоб криволінійний інтеграл по будь-якому замкнутому контуру дорівнював нулю. Відповідь на це питання дає наступна теорема:
Теорема. Нехай у всіх точках деякої області
функції
і
разом зі своїми приватними похідними
,
безперервні. Тоді, для того щоб криволінійний інтеграл по будь-якому замкнутому контуру
, який лежить в цій області, дорівнював нулю, т. е. щоб
,необхідно і достатньо виконання рівності
у всіх точках області
.
Доведення. Розглянемо довільний замкнутий контур
в області D і запишемо для нього формулу Гріна:
.
Якщо виконується умова (3), то подвійний інтеграл, що стоїть ліворуч, тотожно дорівнює нулю і, отже,
Таким чином, достатність умови (3) доведена.
Доведемо тепер необхідність його запровадження, тобто доведемо, що якщо рівність (2) виконується для будь-якої замкнутої кривої
в області
, то в кожній точці цієї області виконується і умова (3).
Припустимо, навпаки, що рівність (2) виконується, т. Е.
,
а умова (3) не виконується, т. е.
хоча б в одній точці. Нехай, наприклад, в деякій точці
.
Так як в лівій частині нерівності варто безперервна функція, то вона буде позитивна і більше деякого числа
у всіх точках деякої досить малої області
, містить точку
. Візьмемо подвійний інтеграл по цій області від різниці
. Він буде мати позитивне значення. дійсно,
.
Але за формулою Гріна ліва частина останнього нерівності дорівнює криволинейному інтегралу по кордоні
області
, який, за припущенням, дорівнює нулю. Отже, остання нерівність суперечить умові (2), і значить, припущення, що
відмінно від нуля хоча б в одній точці, невірно. Звідси випливає, що
у всіх точках даної області
, а отже
.
Схожі статті