Серед різних видів відносин між поняттями слід звернути особливу увагу на ставлення підпорядкування. Як вже говорилося, поняття з меншим обсягом називаються видовими. а поняття з більшим обсягом - родовими. причому обсяг видового поняття завжди повністю включається в обсяг родового.
Видові і родові поняття тісно пов'язані між собою логічними операціями обмеження і узагальнення.
Так само, якщо до змісту поняття геометрична фігура додати ознака «мати рівні сторони і прямі кути». то воно перетвориться в поняття квадрат. яке буде видовим по відношенню до вихідного родового поняття геометрична фігура:
Ланцюжки обмежень і узагальнень понять
Обмеження і узагальнення понять складаються в логічні ланцюжки, в яких кожне поняття (за винятком початкового і кінцевого) є видовим по відношенню до одного сусіднього поняттю і родовим по відношенню до іншого. Наприклад, якщо послідовно узагальнювати поняття Сонце. то вийде наступний ланцюжок:
Солнце® зірка ® небесне тело® фізичне тіло ® форма матерії
У цьому ланцюжку, як бачимо, поняття зірка є родовим по відношенню до поняття Сонце. але видовим по відношенню до поняття небесне тіло; так само поняття небесне тіло є родовим по відношенню до поняття зірка. але видовим по відношенню до поняття фізичне тіло і т.д. Зрозуміло, що рух по нашому ланцюжку від поняття Сонце до поняття форма матерії являє собою серію послідовних узагальнень, а рух в зворотному напрямку - обмежень.
# 8252; # 8252; (Якщо зобразити відносини між поняттями з вказаною ланцюжка на схемі Ейлера, то вийдуть кола, послідовно розташовані один в іншому: найменший позначає поняття Сонце. А найбільший - форма матерії).
Межею ланцюжка обмеження будь-якого поняття завжди буде якесь одиничне поняття, а межею ланцюжка узагальнення, як правило, буде якесь широке, філософське поняття (наприклад, об'єкт світобудови, форма матерії або форма буття).
Найбільш часті помилки, які допускають при обмеженні і узагальненні понять, полягають в тому, що замість виду для якогось роду називають частину з деякого цілого, і замість роду для якогось виду називають ціле по відношенню до будь-якої частини. Наприклад, в якості обмеження поняття квітка пропонують поняття стебло. Стебло, звичайно ж, є частиною квітки, але обмежити поняття - це значить підібрати не частина для цілого, а вид для роду, тобто правильним обмеженням поняття квітка буде поняття ромашка або тюльпан, або хризантема і т.п. Так само, наприклад, як узагальнення поняття дерево нерідко пропонують поняття ліс. Звичайно ж, ліс є певним цілим по відношенню до дерев, з яких він складається, але узагальнити поняття - це значить підібрати не ціле для частини, а рід людське око, тобто правильним узагальненням поняття дерево буде поняття рослина або об'єкт флори. або живий організм і т.п.
Отже, майже будь-яке поняття можна як обмежити, так і узагальнити. Це означає підібрати для нього як видове поняття, так і родове. Наприклад, обмеженням поняття людина буде поняття спортсмен (або письменник. Або чоловік. Або молода людина і т.п.), а його узагальненням буде поняття жива істота:
Вище було сказано, що обмежити і узагальнити можна майже будь-яке поняття. Правильніше було б стверджувати, що переважна більшість понять можна піддати логічних операцій обмеження і узагальнення. Які ж поняття не можете заборонити або узагальнити? Ми їх вже згадували - це одиничні поняття або широкі, філософські поняття, на яких закінчується будь-яка логічний ланцюжок обмеження або узагальнення. Поодинокі поняття неможливо обмежити (проте їх можна послідовно, поетапно узагальнювати аж до якогось широкого, філософського поняття), а філософські, гранично широкі за обсягом поняття неможливо узагальнити (але їх можна послідовно обмежувати аж до якогось одиничного поняття).
Однією з важливих логічних операцій з поняттями, яка постійно використовується як в науковому, так і в повсякденному мисленні, є операція визначення поняття. У житті ми часто зустрічаємося з такими виразами, як «почнемо з визначення ...», «дайте визначення ...», «запам'ятайте визначення ...», «це невірне визначення ...» і т.п. Що ж таке визначення? Давайте дамо визначення визначенню.
Явна визначення ставить собі за мету безпосереднє розкриття змісту нікого поняття, пряму відповідь на питання, чим є об'єкт, який воно позначає. Наприклад, визначення: Термометр - це фізичний прилад, призначений для вимірювання температури - явне.
Визначення також бувають реальними і номінальними.
Номінальна (від лат. Nomen - ім'я) розкриває значення терміна, в якому виражено якесь поняття. Говорячи простіше, реальні визначення присвячені об'єктам, а номінальні - термінам (словами). Наприклад, визначення: Термометр - це фізичний прилад, призначений для вимірювання температури - реальне, а визначення: Слово «термометр» позначає фізичний прилад, призначений для вимірювання температури - номінальне. Як бачимо, принципової різниці між реальними і номінальними визначеннями не існує. Вони розрізняються, як правило, за формою, але не за суттю.
1. Визначення не повинно бути широким. тобто визначення не повинно перевищувати своїм обсягом визначається поняття. Наприклад, визначення: Сонце - це небесне тіло є широким. визначення - небесне тіло - за обсягом набагато більше визначається поняття - Сонце. З наведеного як приклад визначення далеко не цілком зрозуміло, що таке Сонце, адже небесне тіло - це і будь-яка планета, і будь-яка галактика і т.д. і т.п. В даному випадку можна також сказати, що користуючись класичним способом визначення, ми підвели визначається поняття Сонце під родове поняття небесне тіло. але не зробили другий крок - не вказали на його видову відмінність.
# 8252; # 8252; Наведемо ще кілька прикладів правильних визначень, а також - визначень, в яких порушені розглянуті правила і допущені ралічние помилки.
а) Доба - це відрізок часу, протягом якого Земля робить повний оборот навколо своєї осі (правильне визначення).
б) Жанр - це стійка форма будь-якого твору мистецтва (правильне визначення).
в) Собака - це друг людини (двозначне визначення).
г) Творче мислення - це мислення, яке забезпечує рішення творчих завдань (коло у визначенні).
д) Революція - це велике історична подія, в результаті якого в суспільстві змінюється політична влада (вузьке визначення).
е) Безхазяйне майно - це майно, яке має власника або власник якого невідомий (правильне визначення).
ж) Кінь - це ссавець хребетна тварина (широке визначення).
з) Суфікс - це виділяється в складі словоформи послекорневая афіксальних морфема (некомунікабельності визначення).
Поділ поняття складається з трьох частин: 1. ділене поняття, 2. результати розподілу, 3. підставу розподілу (ознака, за якою здійснюється поділ). Наприклад, в наступному розподілі: Люди бувають чоловіками і жінками (або, що те ж саме: Люди діляться на чоловіків і жінок) діленим є поняття люди. результати розподілу - це поняття чоловіки і жінки. а підстава даного поділу - підлогу, тому що люди в ньому розділені за статевою ознакою. Залежно від підстави розподіл може бути різним. Наприклад: Люди бувають високими, низькими і середнього зросту (підстава поділу - зростання); Люди бувають монголоидами, европеоидами і негроїдами (підстава поділу - раса); Люди бувають вчителями, лікарями, інженерами і т.д. (Підстава поділу - професія).
Іноді поняття ділиться дихотомически. тобто в перекладі з грецького, навпіл, по типу А і не-А. наприклад: Люди бувають спортсменами і не спортсменами. Дихотомічне розподіл завжди правильне, тобто в ньому автоматично виключаються всі можливі в розподілі помилки, про які йтиметься далі.
Ми добре знаємо, навіщо нам потрібна операція визначення поняття: будь-яке знайомство з будь-яким новим предметом починається з визначення. Тепер відповімо на запитання, яку роль в мисленні і мові виконує операція поділу поняття. Вивчаючи різні науки, ви помітили, що жодна з них не обходиться без різних класифікацій, тобто розділень якихось областей дійсності на групи, частини, види і т.п. (Класифікація рослин в ботаніці, тварин - в зоології, хімічних елементів - в хімії і т.д.). Однак будь-яка класифікація - це не що інше, як логічна операція поділу поняття. Тільки класифікації можуть бути великими, докладними, науковими, але також можуть бути простими, повсякденними, повсякденними. Коли ми говоримо: Люди діляться на чоловіків і жінок або Навчальні заклади бувають початковими, середніми та вищими, то в цьому випадку вже створюємо нехай маленьку і просту, але - класифікацію. Отже, логічна операція поділу поняття лежить в основі будь-якої класифікації, без якої не обходиться жодне наукове, ні повсякденне мислення.
Існує кілька логічних правил поділу поняття. Порушення хоча б одного з них призводить до того, що обсяг поняття не розкривається, і поділ не досягає своєї мети, будучи неправильним. Розглянемо ці правила і помилки, що виникають при їх порушенні.
1. Розподіл має проводитися по одній підставі. тобто при розподілі поняття слід дотримуватися тільки одного вибраної ознаки. Наприклад, в розподілі: Люди бувають чоловіками, жінками і вчителями використовуються два різних підстави - підлогу і професія, що неприпустимо. Помилка, що виникає при порушенні цього правила, називається підміною підстави. У розподілі з підміною підстави може використовуватися не тільки два різних підстави, як у наведеному вище прикладі, але і більше. Наприклад, в розподілі: Люди бувають чоловіками, жінками, китайцями і блондинами. як бачимо, використовуються три різних підстави - стать, національність і колір волосся, що, звичайно ж, теж є помилкою.
2. Розподіл має бути повним. тобто треба перерахувати всі можливі результати розподілу (сумарний обсяг усіх результатів розподілу повинен бути дорівнює обсягу вихідного діленепоняття). Наприклад, поділ: Навчальні заклади бувають початковими і середніми є неповним. тому не вказано ще один результат ділення - вищі навчальні заклади. Але як бути, якщо треба перераховувати не два чи три, а десятки або сотні результатів розподілу. В цьому випадку можна вживати поняття: і інші, і інші, і так далі, і тому подібне, які будуть включати в себе не перераховані результати розподілу. Наприклад: Люди бувають росіянами, німцями, китайцями, японцями і представниками інших національностей.
3. Результати розподілу не повинні перетинатися, тобто поняттям, що представляє собою результати розподілу, слід бути несумісними, їх обсяги не повинні мати спільних елементів (на схемі Ейлера кола, що позначають результати розподілу, не повинні стикатися, розташовуючись окремо один від одного). Наприклад, в розподілі: Країни світу поділяються на північні, південні, східні і західні допущена помилка - перетин результатів розподілу. На перший погляд наведене в якості прикладу розподіл здається безпомилковим: воно проведено за однією підставою (сторона світла) і є повним (всі сторони світу перераховані). Щоб побачити помилку в даному розподілі треба міркувати так. Візьмемо якусь країну, наприклад, Канаду і відповімо на питання - чи є вона північній? Звичайно, є, тому що розташована в північній півкулі Землі. Тепер відповімо на запитання, чи є Канада західною країною? Так, тому що вона розташована в західній півкулі Землі. Таким чином, виходить, що Канада - одночасно і північна, і західна країна, тобто вона є загальним елементом обсягів понять північні країни і західні країни, а значить, ці поняття, а вірніше їх обсяги, перетинаються. Те ж саме можна сказати і щодо понять південні країни і східні країни. На схемі Ейлера результати розподілу з нашого прикладу будуть розташовуватися так:
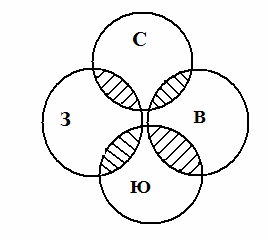
Згадаймо, кожна класифікація побудована таким чином, що будь-який елемент, що потрапляє в одну купку (частина, вид), ні в якому разі не потрапляє в інші. Це і є наслідок неперетинання результатів поділу або їх взаємовиключення при складанні будь-якій класифікації.
4. Поділ має бути послідовним, тобто не допускає пропусків і стрибків. Розглянемо наступний розподіл: Ліси бувають хвойними, листяними, змішаними і сосновими. Явно зайвим тут виглядає поняття соснові ліси. в силу чого допущена в розподілі помилка нагадує підміну підстави (див. перше правило). Однак підстава в даному випадку не змінювалося: поділ було проведено по одному і тій же підставі - тип деревних листя. Підміна підстави присутній в такому, наприклад, поділ: Ліси бувають хвойними, листяними, змішаними, підмосковним і тайговими. (Розподіл проведено за двома різними підставами - тип деревних листя і географічне місцезнаходження лісу). Повернемося до нашого першого прикладу. Правильно було б розділити лісу на хвойні, листяні і змішані, а потім провести другий розподіл - розділити хвойні ліси на соснові і ялинові. Таким чином, треба було зробити два послідовних розподілу, а в наведеному прикладі друге розподіл пропущено, через нього як би перескочили, в результаті чого дві поділки змішалися в одне. Така помилка називається стрибком у поділі. Ще раз відзначимо, що стрибок у поділі не слід плутати з підміною підстави. Наприклад, в розподілі: Навчальні заклади бувають початковими, середніми, вищими і університетами присутній стрибок, а в розподілі: Навчальні заклади бувають початковими, середніми, вищими і комерційними допущена підміна підстави.
# 8252; # 8252; Наведемо ще кілька прикладів правильного розподілу, а також - ділення, в якому порушені розглянуті правила і допущені різні помилки.
а) Транспорт буває наземним, підземним, водним, повітряним, громадським і особистим (підміна підстави).
б) За темпераментом люди діляться на сангвініків, меланхоліків, флегматиків і холериків (перетин результатів розподілу).
в) Геометричні фігури діляться на плоскі, об'ємні, трикутники і квадрати (стрибок у поділі).
г) Відбір в живій природі буває штучним або природним (правильне розподіл).
д) Художні романи бувають пригодницькими, детективними, фантастичними, історичними, любовними та іншими (перетин результатів розподілу).
е) Запам'ятовування бувають довільними і мимовільними (правильне розподіл - дихотомічне).
ж) Математичні дії діляться на додавання, віднімання, множення, ділення, піднесення до степеня, добування кореня і знаходження логарифма (правильне розподіл).
з) Тварини діляться на хижаків, травоїдних, всеїдних і ссавців (підміна підстави).
і) Енергія буває механічної і хімічної (неповне поділ).