Поняття «стохастичний процес» відноситься до області хаосу, до безладного поведінки, до процесу, динаміка якого випадкова і непередбачувана. Відомим прикладом такого процесу є броунівський рух.
Слово "резонанс" в найзагальнішому сенсі означає сильний відгук будь-якої системи на невелику зовнішній вплив. Важливим є те, що такий сильний відгук - вибірковий, тобто він виникає тільки при певних параметрах зовнішнього впливу. Резонанс виникає, якщо частота зовнішнього впливу порівнюється з власною частотою коливань системи.
Разом же ці два слова означають дуже цікаве і, на перший погляд, суперечить здоровому глузду явище, яке має місце в багатьох, зовсім різних системах і навіть, як виявляється, вже давно використовується природою.
Дане явище було відкрито в 80-х роках. Суть стохастичного резонансу полягає в тому, що додавання в систему шуму, тобто хаотичного руху, не зменшує, а навпаки посилює відгук системи на слабке періодичне вплив. При цьому шум не тільки не пригнічує сигнал, а, навпаки, допомагає йому проявитися. Найбільш сильний ефект виникає при деякій цілком певної, оптимальної інтенсивності шуму.
Будь-якому, хто стикався з проблемою виділення корисного сигналу з шуму, здається очевидним твердження, що першим кроком в цьому процесі є максимально можливе зменшення інтенсивності шуму. Ще з тих часів на зорі радіотехніки, коли інженери вперше почули лунає з динаміків шипіння, вони шукають способи придушення шумів, що неминуче виникають в електричних ланцюгах і комунікаційних системах. Вважається, що генерувати шум необхідно лише в ситуаціях, коли потрібно не дати комусь надійно прийняти корисний сигнал.
Ідея використовувати шум для поліпшення якості сигналу здається абсурдною, адже жодній нормальній людині не прийде в голову, наприклад, дряпати компакт-диск, щоб з нього стала краще зчитуватися інформація. Однак дослідження останніх років дозволяють зробити висновок, що в певних випадках шум може відігравати конструктивну роль при сприйнятті слабких сигналів завдяки ефекту, який отримав назву "стохастичний резонанс". Явище виявилося настільки незвичним, що перший час після відкриття воно привертало увагу дуже обмеженого кола вчених, в основному тих, хто його і виявив.
Стохастичний резонанс - це посилення періодичного сигналу під дією білого шуму певної потужності. Є універсальним явищем, властивим багатьом нелінійних систем, що знаходяться під зовнішнім впливом одночасно хаотичного і слабкого періодичного впливу.
Для пояснення цього явища розглянемо будь-яку бістабільності систему, що володіє диссипацией, тертям. Під дією достатнього зовнішнього впливу така система може перейти в інший стан. Якщо достатня зовнішній вплив періодичне, то система, так само, буде періодично переходити з одного стану в інший. Недостатнє (подпороговое) вплив не викличе відгуку такої системи. Якщо зовнішній вплив безладно (шум), то система хаотично «блукає», і через невизначений час, середня довжина якого залежить від потужності шуму, може перескочити з одного положення в інше. Динаміка таких стрибків буде безладної.
Розглянемо тепер сумарний ефект підпорогового періодичного і хаотичного впливів. Само по собі подпороговое періодичне обурення не зможе перекинути систему в інший стан, однак шум допомагає цьому, підбиваючи вплив до «критичного» станом. В результаті у відгуку системи проявляється періодичність, обумовлена слабким періодичним впливом.
Оптимальною (яка призводить до максимального відношенню сигналу до шуму) є така потужність шуму, при якій характерний час життя системи в одному стані дорівнює половині періоду періодичного обурення. Занадто сильний або занадто слабкий шум призводять до меншої чутливості системи до слабкого періодичному впливу.
Умовою для виникнення стохастичного резонансу - система повинна бути нелінійної, інакше відгук системи на сумарний вплив буде просто сумою відгуків і не призведе до жодних нових ефектів.
Система повинна володіти, принаймні, двома стабільними або метастабільними станами. Це може бути як бістабільних система, так і система з довготривалим метастабільним збудженим станом.
До систем, що демонструє стохастический резонанс, відносяться, наприклад: динаміка льодовикових періодів на Землі; динаміка північноатлантичного клімату; накачування в кільцевому лазері; органи чуття у ряду тварин.
Розглянемо для прикладу будь-яку бістабільності систему. Слова "бістабільних система" - це система з двома положеннями стійкої рівноваги. Простий механічний приклад - це рух матеріальної точки в потенціалі з двома мінімумами (див. Мал.1а). Якщо на частку діє ще і сила тертя, то ясно, що які б ми не вибрали початкові умови, коливання, в кінці кінців, затухнуть, частка "звалиться" в одну з потенційних ям і буде перебувати там необмежено довго.
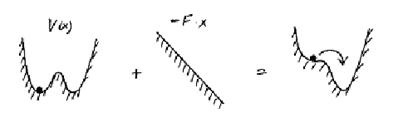
Мал. 14.6 Приклад поведінки бістабільною системи при зовнішньому на неї вплив.
Для того, щоб частка все-таки потрапила в іншу потенційну яму, треба прикласти зовнішню силу. Якщо ця сила досить велика, то вона "витягне" частку з першої ями і перекине її в другу. Мовою потенціалу (в даному тексті потенціал використовується як синонім потенційної енергії) "докласти зовнішню силу" означає додати лінійно зростаючий потенціал, як це показано на рис. 14б. Якщо V (x) - бістабільний потенціал, то зовнішня сила повинна перевершувати величину = | V '(x) |, взятої в точці перегину, тобто там, де повертає сила, створювана потенціалом, найбільша. Тоді сумарний потенціал модифікується так, як показано на малюнку, і частка скотиться в другу яму. Якщо зовнішня сила буде періодична за часом, то в результаті частка буде "скакати" з однієї ями в іншу і назад. В результаті бістабільних система буде відгукуватися на сильне зовнішнє вплив. При цьому частота, з якою система перескакує з одного стійкого стану в інше, збігається з частотою зовнішньої дії. Якщо зовнішній вплив дуже сильне, то система буде слухняно повторювати всі зміни і коливання цієї сили. Якщо зовнішній вплив виявиться не настільки сильним, тобто <, то частица не сможет покинуть яму и останется в ней, несмотря на внешнее воздействие.
Таким чином, бістабільних система може володіти певним порогом чутливості: при зовнішній силі> система починає перескакувати з одного стану в інший з частотою зовнішньої сили, а при <система не чувствует внешнее воздействие. То есть, у бистабильной системы существует некий порог чувствительности к внешним воздействиям. Слишком слабые, т.е. подпороговые воздействия остаются для системы незамеченными, но при дополнительном воздействии на такую систему, даже стохастическим сигналом может происходить усиление сверхслабых сигналов.
Мал. 14.7 Сигнали а) і їх Фур'є-образи б).
Стохастичний сигнал має природу випадкового шуму. За допомогою перетворення Фур'є можна відокремити періодичний сигнал від шуму.
У розглянутій бістабільною системі під дією випадкової силою відбуватимуться випадкові коливання. При цьому може виявитися так, що частка, блукаючи по одній потенційній ямі, раптом перескочить і в другу. Очевидно, що чим сильніше шум, тим менше час перескоку, тобто тим частіше частка перескакує з однієї ями в іншу. Якщо зобразити залежність координати частинки від часу, то вийде приблизно така картина, як на рис. 14.8.
Мал. 14.8 Відгук системи на випадкове зовнішній вплив.
Якщо до зовнішнього шуму додати і слабкий, підпороговий періодичний сигнал, то частка буде як і раніше скакати з однієї ями в іншу, але характер цього процесу зміниться: в ньому з'явиться періодична компонента з періодом, рівним періоду зовнішнього слабкого сигналу. Тобто, переходи здійснюються за рахунок випадкової сили, а періодична добавка лише "модулює" ефект (тобто додає свою власну періодичність).
Шум як би усуває нездоланний раніше потенційний бар'єр і змушує систему відгукуватися на підпороговий сигнал.
У цьому полягає суть стохастичного резонансу (посилення). Особливість стохастичного резонансу полягає в тому, що існує якась оптимальна інтенсивність шуму, при якій відгук системи на періодичний сигнал найсильніший. Для того, щоб визначити, наскільки великий цей відгук, потрібно побудувати залежність координати частинки від часу і за допомогою перетворення Фур'є виділити періодичну складову сигналу. Тоді амплітуда додаткового "горба" Фур'є-образу (рис. 14.7) буде служити кількісною характеристикою чутливості системи. Чим вище горб, тим сильніше виявляється зовнішній періодичний сигнал в русі частинки.
Мал. 14.9 Відгук бістабільною системи при різній інтенсивності шуму.
На малюнку показана залежність координати частинки від часу при одному і тому ж слабкому періодичному сигнал, але при різних інтенсивностях шуму. Видно, що коли інтенсивність шуму мала, частка довго знаходиться в одній потенційній ямі, перш ніж перестрибнути в іншу (рис. 14.9, нижній графік). Зовнішній періодичний сигнал тут ніяк не проявляється. Коли збільшується інтенсивність шуму до оптимальної, частка під сумарним впливом шуму і періодичної сили буде синхронно стрибати з однієї ями в іншу (рис. 14.9, середній графік). Явно видно періодична складова відгуку системи, період якої збігається з періодом зовнішньої сили. Нарешті, при подальшому посиленні шуму рух частинки стане все більш і більш хаотичним; періодична компонента у відгуку буде зменшуватися (рис. 14.9, верхній графік).
Типова залежність відгуку системи від інтенсивності зовнішнього шуму показана на рис. 14.10. Видно, що при деякій інтенсивності шуму відгук системи на корисний сигнал буде максимальним.
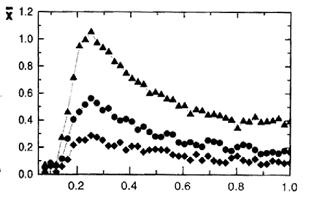
Мал. 14.10 Залежність від інтенсивності шуму амплітуд сигналів періодичної складової.
Певної інтенсивності шуму відповідає цілком конкретне середній час перескоку з однієї ями в іншу. Умова для оптимальної інтенсивності шуму: потрібно щоб викликається цим шумом час перескока дорівнювало половині періоду слабкого періодичного обурення. Коли період перескоку і період зовнішньої сили синхронізовані, виникає найбільш сильний відгук системи на зовнішнє періодичне обурення (резонанс). Якщо ці два процеси не синхронізовані, чутливість до слабкої періодичної силі зменшується.
Стохастичний резонанс використовується в техніці, спостерігається і в функціонуванні живих організмів. Наприклад, стохастичний резонанс застосовується в оптичних системах і виникає при генерації нервових імпульсів.
Прикладом оптичної системи, в якій спостерігався стохастичний резонанс, служить так званий кільцевий лазер (рис.), В якому лазерне світло накачується в резонаторі з трьома або більше дзеркалами. У цій системі існує два стабільних режиму накачування лазерного світла, коли світло рухається у напрямку руху годинникової стрілки або проти. Це був один з перших експериментів (1988 рік), коли стохастический резонанс спостерігався в лабораторії.
На початку 90-х років було усвідомлено, що стохастичний резонанс може грати ключову роль в нейрофізіологічних процесах, а саме, у функціонуванні нейронних мереж, в передачі імпульсів від однієї групи нейронів інший.
Зовсім недавно, у другій половині 90-х років, постало питання про можливість існування стохастичного резонансу на квантовому рівні. Очікується, що квантове "тремтіння частинок", яке існує завжди, навіть при абсолютному нулі температури, і яке відіграє тут роль шуму, сприятиме детектування квантового сигналу, поширенню інформації та т.д.
Стохастичний резонанс може виникати і в системах, відмінних від бістабільних. Головна вимога - це наявність будь-якого порога. Прикладом такої системи може служити система, в якій переходи відбуваються не між двома стійкими положеннями рівноваги, а між "основним" і "порушеними" станами системи.
Нещодавно було описано явище, назване "подвійним стохастичним резонансом". Тут на вільну частку діють відразу два типи шумів: перший створює щось на зразок бістабільності потенціалу, а другий змушує частку в цьому псевдопотенціалу скакати. Явище дуже цікаве, оскільки воно служить прекрасною ілюстрацією того, що шум може не тільки руйнувати тонкі, скоррелировать процеси, а й навпаки - давати їм життя.
Цікаво, що вже в найближчому майбутньому, коли сверхминиатюрная електроніка вийде з наукових лабораторій і стане доступною масовому користувачеві, стохастичний резонанс може виявитися важливою її частиною.
Інший приклад дають нейронні мережі - електронні пристрої, здатні ефективно обробляти величезні обсяги інформації. У таких мережах стохастический резонанс буде проявлятися у вигляді поліпшеної провідності зашумленной інформації і синхронізації процесів, які відбуваються в різних частинах мережі.
В останні роки з'явилася низка повідомлень про успішне використання стохастичного резонансу при обробці сигналів і комп'ютерному розпізнаванні зображень.
Повернутися в зміст: Сучасні фундаментальні та прикладні дослідження в приладобудуванні