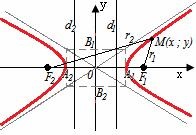
Гіпербола - геометричне місце точок, для кожної з яких модуль різниці відстаней від неї до двох даних точок F1, F2 (фокуси) є величина постійна, рівна 2a.
- асимптоти
- ексцентриситет (c> a). Його можна розглядати, як числову характеристику величини розчину кута між асимптотами.
r1 = ± (# 949; x-a), r1 = ± (# 949; x + a), - фокальні радіуси (верхній знак відповідає правій, нижній - лівої галузі)
- директриси
Геометричний сенс уявної осі показаний на малюнку пунктирною лінією (відстань між асимптотами).
Канонічне рівняння гіперболи (координатні осі збігаються з осями гіперболи):
Властивості рівносторонній гіперболи
Уявна вісь 2b може бути більше, менше або дорівнює дійсної осі 2a. Якщо дійсна і уявна осі рівні (a = b), то гіпербола називається равносторонней (або равнобочной). Ексцентриситет рівносторонній гіперболи дорівнює sqrt (2).
Асимптоти рівносторонній гіперболи взаємно перпендикулярні.
Парні гіперболи
Дві гіперболи називаються сполученими, якщо вони мають загальний центр і загальні осі, але дійсна вісь однієї з них є уявною віссю інший. Парні гіперболи мають загальні асимптоти.
Рівняння гіперболи, пов'язаною даної:
Дійсна вісь цієї гіперболи дорівнює уявної осі інший.
см. Криві другого порядку (Еліпс, Окружність, Гіпербола, Парабола).