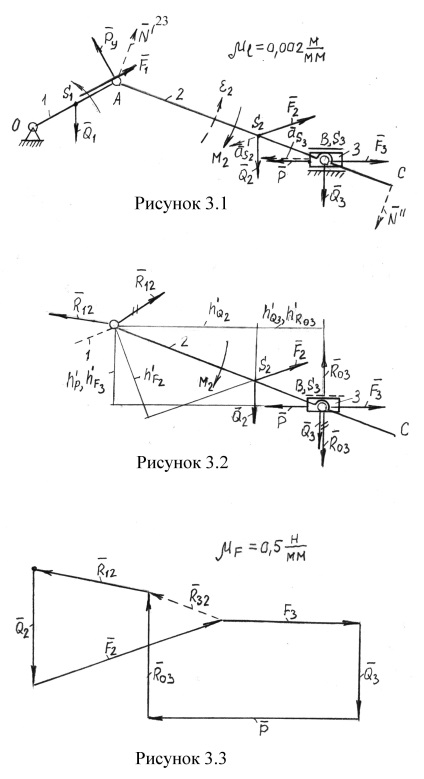
Відомі такі параметри механізму (рис. 3.1): (Всі прискорення беруться з першого листа курсового проекту).
Потрібно визначити реакції в кінематичних парах і врівноважує силу.
Изображаем механізм в заданому положенні з позначенням масштабного коефіцієнта м / мм. який в даному випадку означає, що механізм зменшений в два рази. На механізм діють наступні сили.
1.Сила корисного опору. вказується в завданні. Вона прикладена в точці В повзуна 3 і спрямована горизонтально.
2.Сіли тяжкості. визначаються через маси ланок, які можна умовно визначити за формулою. де q-маса одиниці довжини ланки, l-довжина ланки
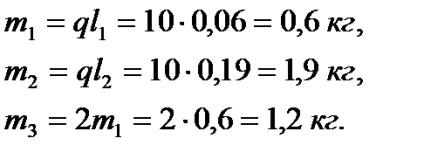
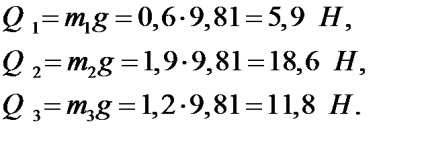
Сили тяжіння прикладаються в центрах мас S1. S2. S3 і спрямовані вертикально вниз.
3.Сила інерції ланок. визначаються за формулою
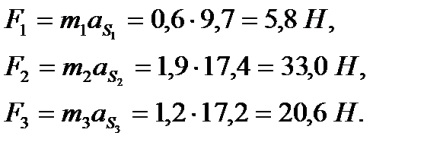
Ці сили прикладаються в центрах мас і спрямовані вони в сторони, зворотні прискорень. (Бажано план прискорень з першого листа перенести на другий лист).
4.Момнети сил інерції М. які можна знайти за формулою. де IS-момент інерції ланок щодо центральних осей
Моменти інерції ланок визначаємо за формулою
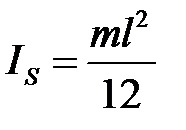
.
Моменти сил інерції М спрямовані в сторони, зворотні кутових прискорень.
5. врівноважується сила. прикладається в точці А кривошипа 1 і спрямована перпендикулярно йому. Нехай у нашому прикладі вона спрямована вгору.
Всі сили і моменти вказуємо на механізмі, причому довжини векторів беремо довільно.
Изображаем окремо структурну групу, що складається з шатуна 2 і повзуна 3 (рис. 3.2). Реакцію направляємо поки довільно, а реакцію вертикально. Нехай вона спрямована вниз. Розглядаємо рівновагу групи і записуємо рівняння моментів відносно точки А. Для цього спочатку з точки А проводимо перпендикуляри до всіх сил, заміряємо їх довжини в міліметрах і множимо на. отримуючи їх величини:
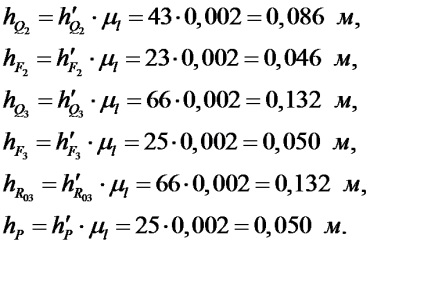
Рівняння рівноваги матиме вигляд:
Так як ця сила виявилася негативною, то вектор ми зачеркиваем (прати не можна!) І направляємо в іншу сторону.
Використовуючи графічне умова рівноваги групи. складаємо силовий багатокутник (рис. 3.3) в масштабі.
Обчислюємо довжини векторів сил
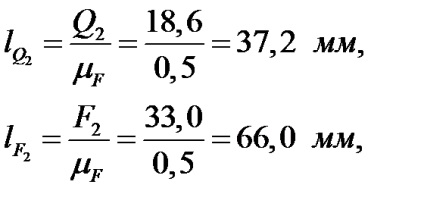
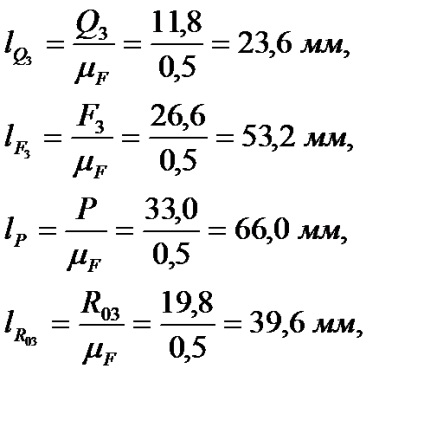
Сили в багатокутнику йдуть в будь-якому порядку, але бажано, щоб спочатку йшли всі сили однієї ланки, а потім сили, що діють на іншу ланку. Якщо довжина вектора сили виявиться менше 3 мм, то замість цієї сили ставимо крапку, біля якої записуємо позначення сили. Початок першої сили (в даному випадку це сила) позначаємо точкою. З'єднуємо кінець останньої сили (у нас це) з початком першої, отримуючи вектор. який спрямований на початок сили. Заміряємо довжину цього вектора в міліметрах і множимо на. отримуючи величину сили
Вектор в точці А перекреслюємо і направляємо його так, як він йде в багатокутнику.
Щоб отримати реакцію в шарнірі В, потрібно розглянути рівновагу однієї ланки, наприклад, другого. Для цього початок сили потрібно з'єднати з кінцем сили. Отримуємо вектор. який йде в початок сили. Заміряємо довжину цього вектора і множимо на. отримуючи значення сили
Изображаем окремо кривошип 1 з усіма силами (рис. 3.4.), Причому реакцію направляємо поки довільно, а сила спрямована в бік, протилежний силі. тобто .З точки Про проводимо перпендикуляри до всіх сил, заміряємо їх і множимо на. Отримуємо довжини плечей сил.
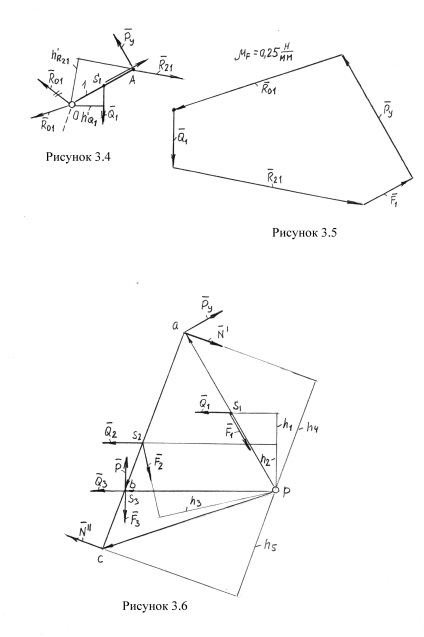
Розглядаючи рівновагу кривошипа, записуємо рівняння моментів щодо точки Про
Використовуємо графічне умова рівноваги кривошипа. будуємо силовий багатокутник в масштабі (рис. 3.5).
Знаходимо довжини векторів
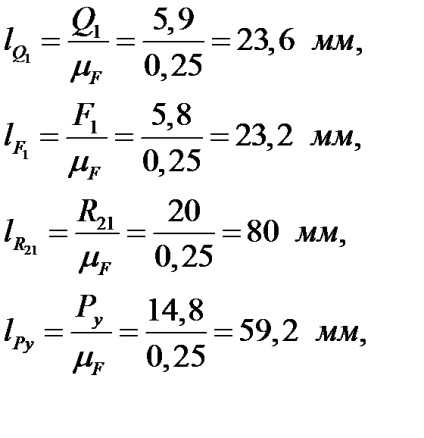
Поєднуючи початок першої сили і кінець останньої. отримуємо вектор. який спрямований на початок сили. Знаходимо величину цієї сили
Вектор в точці О перекреслюємо і направляємо так, як він йде в багатокутнику.
Для перевірки точності розрахунків і побудов знайдемо врівноважуючу силу за методом Жуковського. Момент сили інерції другої ланки замінюємо парою сил і (рис 3.1), що діють, наприклад, в точках А і С і спрямованих перпендикулярно шатуну АС. При цьому напрямок пари сил повинен співпадати з напрямом моменту.
Знайдемо величини цих сил
Переносимо з першого листа курсової роботи план швидкостей, на який поміщаємо все зовнішні сили (рис. 3.6), приклавши їх до відповідних точки і повернувши на 90 # 730; в ту чи іншу сторону. У нашому випадку всі сили повернені за годинниковою стрілкою. З полюса швидкостей р проводимо до сил перпендикуляри, які є плечима сил. Заміряємо довжини перпендикулярів і записуємо рівняння моментів щодо полюси р
Порівняння результатів, отриманих двома способами, говорить про те, що похибка обчислень і побудов незначна.