Перш ніж перейти до вивчення способів представлення графа, розглянемо приклади, дамо визначення графу і ознайомимося з основними поняттями теорії графів. Тут не будуть розглянуті всі аспекти теорії графів (цього і не потрібно), але, по великій частині, ті, що знадобляться нам надалі.
У своєму житті ми, так чи інакше, стикалися з об'єктами, що мають структуру графа. До таких об'єктів належать різного роду маршрути громадського транспорту: система метрополітену, автобусні маршрутом і т.п. Зокрема, програмісту знайома комп'ютерна мережа, яка також є графом (рис. 3.1). Спільне тут це наявність точок, з'єднаних лініями. Так в комп'ютерній мережі точками є окремі сервери, а лініями - різні види електричних сигналів. У метрополітені перше - станції, друге - тунелі, прокладені між ними. В теорії графів точки іменується вершинами, або вузлами. а лінії - ребрами, або дугами. Таким чином, граф - це сукупність вершин, з'єднаних ребрами.
Повернемося до комп'ютерної мережі. Вона володіє певною топологією, і може бути умовно зображено у вигляді деякого числа комп'ютерів і шляхів їх з'єднують. На малюнку нижче як приклад показана полносвязная топологія.
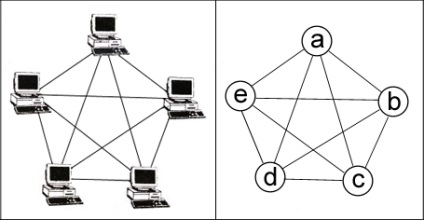
Малюнок 3.1 - Комп'ютерна мережа
Це, по суті, граф. П'ять комп'ютерів є вершинами, а з'єднання (шляхи передачі сигналів) між ними - ребрами. Замінивши комп'ютери вершинами, ми отримаємо математичний об'єкт - граф, який має 10 ребер і 5 вершин. Пронумерувати вершини можна довільним чином, а не обов'язково так, як це зроблено на малюнку.
Ось деякі важливі позначення, які використовуються в теорії графів:
· | V | - порядок (число вершин);
· | E | - розмір графа (число ребер).
У нашому випадку (рис. 1) | V | = 5, | E | = 10;
Коли з будь-якої вершини доступна будь-яка інша вершина, то такий граф називається неорієнтованим зв'язковим графом (рис. 3.1). Якщо ж граф зв'язний, але ця умова не виконується, тоді такий граф називається орієнтованим або Орграф (рис. 3.2). Ребра орграфа прийнято називати дугами.
В орієнтованих і неорієнтованих графах є поняття ступеня вершини. Ступінь вершини - це кількість ребер, що з'єднують її з іншими вершинами. Ступінь входу вершини - кількість вхідних в цю вершину ребер, ступінь виходу - кількість вихідних ребер. Сума всіх ступенів графа дорівнює подвоєній кількості всіх його ребер. Для малюнка 2 сума всіх ступенів дорівнює 20.
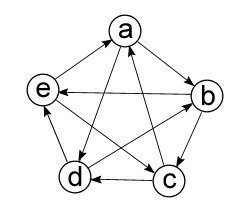
Малюнок 3.2 - Орієнтований граф
У орграфе, на відміну від неориентированного графа, є можливість рухатися з вершини h в вершину s без проміжних вершин, лише тоді коли дуга виходить з h та входить в s. але не навпаки.
Орієнтовані графи мають наступну форму запису:
Третій тип графів - змішані графи (рис. 3.3). Вони мають як спрямовані ребра, так і ненаправлення. Формально змішаний граф записується так: G = (V. E. A), де кожна з букв в дужках позначає те саме, що їй приписувалося раніше.
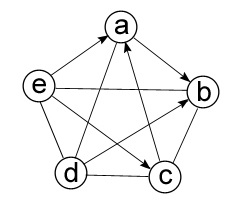
Малюнок 3.3 - Змішаний граф
Коли у ребра обидва кінці збігаються, т. Е. Ребро виходить з деякої вершини F і входить в неї, то таке ребро називається петлею (рис. 3.4).
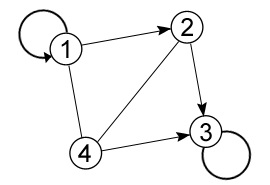
Малюнок 3.4 - Петлі графа
Два або більше графів на перший погляд можуть здатися різними за своєю структурою, що виникає внаслідок різного їх зображення. Але це не завжди так. Візьмемо два графа (рис. 3.5). Вони еквівалентні один одному, адже не змінюючи структуру одного графа можна побудувати інший. Такі графи називаються ізоморфними. т. е. що володіють тим властивістю, що будь-яка вершина з певним числом ребер в одному графі має тотожну вершину в іншому.
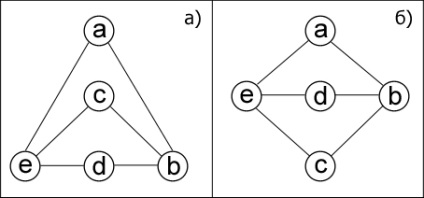
Малюнок 3.5 - ізоморфні графи
Коли кожному ребру графа поставлено у відповідність деяке значення, зване вагою ребра. тоді такий граф зважений. У різних завданнях як ваги можуть виступати різні види вимірювань, наприклад довжини, ціни маршрути і т. П. У графічному поданні графа вагові значення вказуються, як правило, поруч з ребрами.
У будь-якому з розглянутих нами графів є можливість виділити шлях і, причому не один. Шлях - це послідовність вершин, кожна з яких з'єднана з сусідньою вершиною допомогою ребра. Якщо перша і остання вершини збігаються, то такий шлях називається циклом. Довжина шляху визначається кількістю складових його ребер. Наприклад, на малюнку 4.а шляхом служить послідовність [(e), (a), (b), (c)]. Цей шлях є подграфом, так як до нього може бути застосовано визначення останнього, а саме: граф G '= (V'. E ') є подграфом графа G = (V. E), тільки тоді коли V' і E 'належать V. E .
Граф, як і більшість інших математичних об'єктів, може бути представлений на комп'ютері (збережений в його пам'яті). Існують кілька способів його інтерпретації, ось найбільш відомі з них:
Використання двох перших методів передбачає зберігання графа у вигляді двовимірного масиву (матриці). Причому розміри цих масивів, залежать від кількості вершин і / або ребер в конкретному графі. Так розмір матриці суміжності n × n. де n - число вершин, а матриці інцидентності n × m. n - число вершин, m - число ребер в графі.