Спочатку алгеброю називали вчення про рішення рівнянь. За багато століть свого розвитку алгебра перетворилася в науку, яка вивчає операції і відносини на різних множинах. Тому не випадково вже в початковій школі діти знайомляться з такими алгебраїчними поняттями, як вираз (числове і зі змінними), числове рівність, числове нерівність, рівняння. Вони вивчають різні властивості арифметичних дій над числами, які дозволяють раціонально виконувати обчислення. І, звичайно, в початковому курсі математики відбувається їх знайомство з різними залежностями, відносинами, але щоб використовувати їх з метою розвитку розумової діяльності дітей, вчитель повинен опанувати деякими загальними поняттями сучасної алгебри - поняттям відповідності, відносини, алгебраїчної операції та ін. Крім того, засвоюючи математичну мову, що використовується в алгебрі, учитель зможе глибше зрозуміти сутність математичного моделювання реальних явищ і процесів.
Вивчаючи навколишній світ, математика розглядає не тільки його об'єкти, а й головним чином зв'язки між ними. Ці зв'язки називають залежностями, відповідниками, відносинами, функціями. Наприклад, при обчисленні довжин предметів встановлюються відповідності між предметами і числами, які є значеннями їх довжин; при вирішенні задач на рух встановлюється залежність між пройденою відстанню і часом, якщо швидкість руху постійна.
Конкретні залежності, відповідності, відносини між об'єктами в математиці вивчалися з моменту її виникнення. Але питання про те, що загальне мають найрізноманітніші відповідності, якою є сутність будь-якого відповідності, був поставлений в кінці XIX - початку XX століття, і відповідь на нього був знайдений в рамках теорії множин.
У початковому курсі математики вивчаються різні взаємозв'язку між елементами одного, двох і більше множин. Тому вчителю треба розуміти їх суть, що допоможе йому забезпечити єдність в методиці вивчення цих взаємозв'язків.
Розглянемо три приклади відповідностей, що вивчаються в початковому курсі математики.
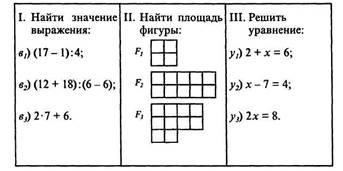
У першому випадку ми встановлюємо відповідність між заданими виразами і їх числовими значеннями. У другому з'ясовуємо, яке число відповідає кожній з даних фігур, характеризуючи її площа. У третьому шукаємо число, яке є рішенням рівняння.
Що спільне мають ці відповідності?
Бачимо, що у всіх випадках ми маємо два безлічі: в першому - це безліч з трьох числових виразів і безліч N натуральних чисел (йому належать значення даних виразів), у другому - це безліч з трьох геометричних фігур і безліч N натуральних чисел; в третьому - це безліч з трьох рівнянь і безліч N натуральних чисел.
Виконуючи запропоновані завдання, ми встановлюємо зв'язок (відповідність) між елементами цих множин. Її можна представити наочно, за допомогою графів (рис. 1).
Можна задати ці відповідності, перерахувавши всі пари елементів, що знаходяться в заданому відповідно:
Отримані безлічі показують, що будь-який відповідність між двома множинами X і Y можна розглядати як безліч впорядкованих пар. утворених з їх елементів. А так як впорядковані пари - це елементи декартова твори, то приходимо до наступного визначення загального поняття відповідності.
Визначення. Відповідністю між елементами безліч X і Y називається всяке підмножина декартова твори цих множин.
Відповідності прийнято позначати буквами Р, S, T, R та ін. Якщо S - відповідність між елементами множин X і Y, то, згідно з визначенням, S Х х Y.
З'ясуємо тепер, як задають відповідності між двома множинами. Оскільки відповідність - це підмножина, то його можна ставити як будь-яка множина, тобто або перерахувавши всі пари елементів, що знаходяться в заданому відповідно, або вказавши характеристичне властивість елементів цієї підмножини. Так, відповідність між множинами X = і Y = можна задати:
1) за допомогою пропозиції з двома змінними: а
2) перерахувавши пари чисел, що належать підмножині декартова твори XxY:. До цього способу завдання відносять також завдання відповідності за допомогою графа (рис. 2) і графіка (рис. 3)
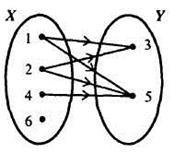
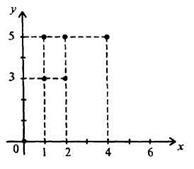
Нерідко, вивчаючи відповідності між елементами множин X і Y, доводиться розглядати і відповідність, йому протилежне. Нехай, наприклад,
S - відповідність «більше на 2» між елементами множин
Х = і Y =. Тоді S = і його граф буде таким, як на малюнку 4а.
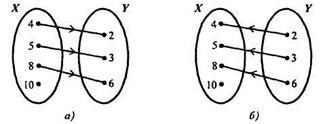
Відповідність, зворотне даному, - це відповідність «менше на 2». Воно розглядається між елементами множин Y і X, і щоб його уявити наочно, досить на графі відносини S напрямок стрілок поміняти на протилежний (рис. 4б). Якщо відповідність «менше на 2» позначити S -1. то S 1 =.
Домовимося пропозицію «елемент х знаходиться у відповідності S з елементом у" записувати коротко так: xSy. Запис xSy можна розглядати як узагальнення записів конкретних відповідностей: х = 2у; х> 3у + 1 та ін.
Скористаємося введеної записом для визначення поняття відповідності, зворотного даному.
Визначення. Нехай S - відповідність між елементами множин X і Y. Відповідність S -1 між елементами множин Y і X називається зворотним даним, якщо yS -x тоді і тільки тоді, коли xSy.
Відповідності S і S -1 називають взаємно зворотними. З'ясуймо особливості їх графіків.
Побудуємо графік відповідності S = (рис. 5а). При побудові графіка відповідності S 1 = ми повинні першу компоненту вибирати з безлічі Y =, а другу - з безлічі X =. В результаті графік відповідності S -1 співпаде з графіком відповідності S. Щоб розрізняти графіки відповідностей S і S -1,
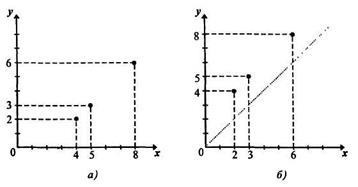
домовилися першу компоненту пари відповідності S -1 вважати абсциссой, а другу - ординатою. Наприклад, якщо (5, 3) S, то (3, 5) S -1. Точки з координатами (5, 3) і (3, 5), а в загальному випадку (х, у) і (у, х) симетричні щодо бісектриси 1-го і 3-го координатних кутів. Отже, графіки взаємно обернених відповідностей S і S -1 симетричні щодо бісектриси 1-го і 3-го координатних кутів.
Щоб побудувати графік відповідності S -1. досить зобразити на координатній площині точки, симетричні точкам графіка S щодо бісектриси 1-го і 3-го координатних кутів.