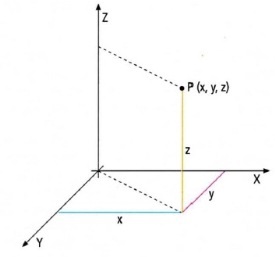
Таким же чином, як була визначена система координат на площині, можна визначити систему координат і в просторі. Єдине, що ми повинні для цього зробити, це провести третю вісь. яку назвемо вісь Z ( «вісь зет»). Вона буде перпендикулярна площині, утвореної двома іншими осями. Третя координата нашої точки - z - буде відповідної висотою по даній осі.
Завдання, в яких задіяні площині і прямі, можуть бути вирішені алгебраїчними методами.
Розмірність простору. Тільки що ми показали, що точка в одновимірному просторі має одну координату: Р (x); в двовимірному просторі дві координати: Р (x, y); а в тривимірному просторі точка позначається трьома координатами: Р (x, y, z). Крім того, для позначення координати може використовуватися буква з нижнім індексом. Так, точку на прямій можна позначити як $ P (x_1) $, точку на площині - як $ P (x_1, x_2) $, точку в просторі - як $ P (x_1, x_2, x_3) $. Але ніщо не заважає нам поговорити про координати точки в чотиривимірному просторі - $ P (x_1, x_2, x_3, x_4) $ - і взагалі в n-вимірному просторі з точками виду $ P (x_1, x_2, ..., x_n) $.
При наявності відповідних визначень можна з однаковою легкістю працювати як в тривимірному, так і в 25-вимірному просторі, і навіть в нескінченновимірних - при відсутності будь-якої математичної суперечливості. Вже починаючи з тривимірного простору, в значній мірі втрачається геометрична інтуїція. це природно. Проте, і в багатовимірних просторах можна застосовувати алгебраїчні методи при вирішенні завдань. Звичайно, складно уявити і визнати існування просторів з розмірністю більше трьох, але це ніяк не заважає працювати з ними математичними методами.
Матеріали по темі:
Поділитися з друзями: