У магічному квадраті 3х3 магічною постійної 15 повинні бути рівні сумі трьох чисел у 8 напрямках: по 3 рядках, 3 стовпцях і 2 діагоналям. Так як число, що стоїть в центрі, належить 1 рядку, 1 колонку і 2 діагоналям, воно входить в 4 з 8 трійок, що дають в сумі магічну постійну. Таке число тільки одне: це 5. Отже, число, що стоїть в центрі магічного квадрата 3х3, вже відомо: воно дорівнює 5.
Розглянемо число 9. Воно входить тільки в 2 трійки чисел. Ми не можемо помістити його в кут, так як кожна кутова клітина належить 3 трійкам: рядку, стовпці і діагоналі. Отже, число 9 має стояти в якійсь клітині, що примикає до сторони квадрата в її середині. Через симетрії квадрата байдуже, яку з сторін ми виберемо, тому пишемо 9 над числом 5, що стоять в центральній клітці. По обидва боки від дев'ятки в верхньому рядку ми можемо вписати тільки числа 2 і 4. Яка з цих двох чисел виявиться в правому верхньому кутку і яке в лівому, знову - таки не має значення, так як одне розташування чисел переходить в інше при дзеркальному відображенні . Решта клітини заповнюються автоматично. Проведене нами просте побудова магічного квадрата 3х3 доводить його єдиність.
Такий магічний квадрат був у древніх китайців символом великого значення. Цифра 5 в середині означала землю, а навколо неї в строгій рівновазі розташовувалися вогонь (2 і 7), вода (1 і 6), дерево (3 і 8), метал (4 і 9).
Зі збільшенням розмірів квадрата (числа клітин) швидко зростає кількість можливих магічних квадратів такого розміру. Існує 880 магічних квадратів порядку 4 і 275 305 224 магічних квадратів порядку 5. Причому, квадрати 5х5 були відомі ще в середні століття. Мусульмани, наприклад, дуже благоговійно ставилися до таких квадратом з цифрою 1 в середині, вважаючи його символом єдності Аллаха.
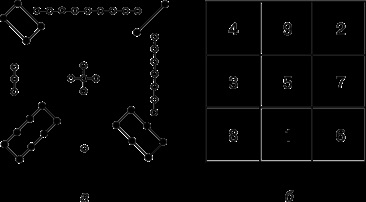
1.2.Магіческій квадрат - давньокитайського походження. Згідно з легендою, за часів правління імператора Ю (бл. 2200 до н.е.) з вод Хуанхе (Жовтої ріки) спливла священна черепаха, на панцирі якої були написані таємничі ієрогліфи (рис. 1, а), і ці знаки відомі під назвою ло-шу і рівносильні магічного квадрату, зображеному на рис. 1, б. У 11 ст. про магічні квадратах дізналися в Індії, а потім в Японії, де в 16 ст. магічним квадратах була присвячена велика література. Європейців з магічними квадратами познайомив в 15 в. візантійський письменник Е.Мосхопулос. Першим квадратом, придуманим європейцем, вважається квадрат А.Дюрера (рис. 2), зображений на його знаменитій гравюрі Меланхолія 1. Дата створення гравюри (1514) вказана числами, що стоять в двох центральних клітинах нижнього рядка. Магічним квадратах приписували різні містичні властивості. У 16 ст. Корнелій Генріх Агріппа побудував квадрати 3-го, 4-го, 5-го, 6-го, 7-го, 8-го та 9-го порядків, які були пов'язані з астрологією 7 планет. Існувало повір'я, що вигравіруваний на сріблі магічний квадрат захищає від чуми.

У 19 і 20 ст. інтерес до магічних квадратах спалахнув з новою силою. Їх стали досліджувати за допомогою методів вищої алгебри.

Єдиний нормальний магічний квадрат 3 × 3. Був відомий ще в Давньому Китаї, перше зображення на черепаховому панцирі датується 2200 до н.е ..
Сучасні математики називають подібні квадрати «досконалими». Стало бути, «досконалий» і «диявольський» для сучасних математиків - синоніми!
Але є ще один МК не менш цікавий, ніж диявольський. Видатний американський масон, вчений, громадський діяч і дипломат Бенджамін Франклін склав квадрат 16 × 16, який крім наявності постійної суми 2056 у всіх рядках, стовпцях і діагоналях мав ще одне додаткове властивість. Якщо вирізати з аркуша паперу квадрат 4 × 4 і укласти цей лист на великий квадрат так, щоб 16 клітин більшого квадрата потрапили в цей проріз, то сума чисел, що з'явилися в цій прорізи, куди б ми її не поклали, буде одна і та ж - 2056.
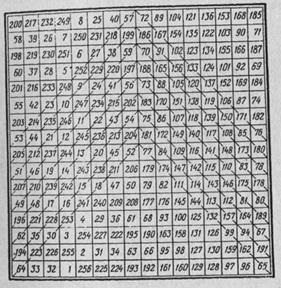
Цей квадрат є магічно-магічним з усіх МК, складених коли-небудь будь-яким магом.
1.4. Магічний квадрат Ян Хуея (Китай). У 13 ст. математик Ян Хуей зайнявся проблемою методів побудови магічних квадратів. Його дослідження були потім продовжені іншими китайськими математиками. Ян Хуей розглядав магічні квадрати не тільки третього, але і високих порядків. Деякі з його квадратів були досить складні, проте він завжди давав правила для їх побудови. Він зумів побудувати магічний квадрат шостого порядку, причому останній виявився майже асоціативним (в ньому тільки дві пари центрально протилежних чисел не дають суму 37):
Сума чисел на будь-який горизонталі, вертикалі і діагоналі дорівнює 34. Ця сума також зустрічається у всіх кутових квадратах 2 × 2, в центральному квадраті (10 + 11 + 6 + 7), в квадраті з кутових клітин (16 + 13 + 4 + 1 ), в квадратах, побудованих «ходом коня» (2 + 8 + 9 + 15 і 3 + 5 + 12 + 14), в прямокутниках, утворених парами середніх клітин на протилежних сторонах (3 + 2 + 15 + 14 і 5 + 8 + 9 + 12). Більшість додаткових симетрій пов'язано з тим, що сума будь-яких двох центрально симетрично розташованих чисел дорівнює 17.
1.5. Квадрати Генрі Е. Дьюдени і Аллана У. Джонсона-мл.
Якщо в квадратну матрицю n × n заноситься не строго натуральний ряд чисел, то даний магічний квадрат - нетрадиційний. Нижче представлені два таких магічних квадрата, заповнені в основному простими числами. Перший має порядок n = 3 (квадрат Дьюдени); другий (розміром 4x4) - квадрат Джонсона. Обидва вони були розроблені на початку двадцятого століття:
Є ще кілька подібних прикладів:
Останній квадрат, побудований в 1913 р Дж.Н.Мансі, примітний тим, що він складений з 143 послідовних простих чисел за винятком двох моментів: залучена одиниця, яка не є простим числом, і не використано єдине парне просте число 2.
У 1917 р на франко-німецькому фронті, унтер-офіцер Франц Буль, займаючись мародерством на поле бою, знайшов в кишені вбитого солдата-індуса довгу смужку щільного паперу, яка була списана квадратами, розділеними на клітини, заповненими арабською в'яззю. Він передав цю смужку німецькому професору, який займався магічними квадратами. Швидше за все, смужка містила талісман, не спас, однак, його володаря від смерті.
Після перекладу з арабської мови, з'ясувалося, що документ містить магічний квадрат 3-го порядку і напівмагічний квадрат 4-го порядку. В квадраті 4 × 4 числа повторюються, і суми діагоналей не збігаються з константою:
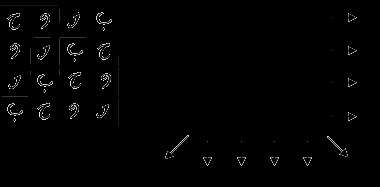
Потім слідував список заклинань, імен богів і демонів, який професор просто відірвав і знищив.
ГлаваII. Основна термінологія
Кожен елемент магічного квадрата називається клітиною. Квадрат, сторона якого складається з n клітин, містить n 2 клітин і називається квадратом n -го порядку.
У більшості магічних квадратів використовуються перші n послідовних натуральних чисел. Сума S чисел, що стоять в кожному рядку, кожному стовпці і на будь-який діагоналі, називається постійної квадрата і дорівнює S = n (n 2 + 1) / 2. Доведено, що n ≥ 3. Залежність постійної квадрата від його порядку можна простежити за допомогою таблиці.
Дві діагоналі, що проходять через центр квадрата, називаються головними діагоналями.
Ламаної називається діагональ, яка, дійшовши до краю квадрата, триває паралельно першому відрізку від протилежного краю (таку діагональ утворюють заштриховані клітини на малюнку.
Клітини, симетричні щодо центру квадрата, називаються кососімметрічнимі. Такі, наприклад, клітини a і b.

ГлаваIII. Способи заповнення магічних квадратів

Магічні квадрати непарного порядку можна побудувати за допомогою методу французького геометра 17 в. А. де ла Лубер (сіамський метод). Розглянемо цей метод на прикладі квадрата 5-го порядку (рис. 4). Число 1 поміщається в центральну клітку верхнього рядка. Всі натуральні числа розташовуються в природному порядку циклічно знизу вгору в клітинах діагоналей справа наліво. Дійшовши до верхнього краю квадрата, продовжуємо заповнювати діагональ, що починається від нижньої клітини у наступній колонці (по ламаній діагоналі). Дійшовши до правого краю квадрата, продовжуємо заповнювати діагональ, що йде від лівої клітини рядком вище. Дійшовши до заповненої клітини або кута, траєкторія спускається на одну клітку вниз, після чого процес заповнення триває.
Для полегшення заповнення квадрата даним методом, а саме визначення місця заповнення наступної клітини, після краю квадрата можна скористатися наступною схемою
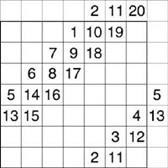
Поставимо 1 в середню клітку верхнього ряду і продовжимо послідовність по діагоналі вправо-вгору. Якщо чергове число на діагоналі виходить за межі квадрата, ми його переставляємо в відповідне поле в квадрат.
Вивчаючи різні джерела, ми звернули увагу на те, що можна заповнювати квадрати і в іншому напрямку і не обов'язково 1 стоїть в даній позиції.
3.2. Метод Ф.де ла Іра (1640-1718) заснований на двох початкових квадратах. На рис. 5 показано, як за допомогою цього методу будується квадрат 5-го порядку. У клітку першого квадрата вписуються числа від 1 до 5 так, що число 3 повторюється в клітинах головної діагоналі, що йде вправо вгору, і жодне число не зустрічається двічі в одному рядку або в одному стовпці. Те ж саме ми робимо з числами 0, 5, 10, 15, 20 з тією лише різницею, що число 10 тепер повторюється в клітинах головної діагоналі, що йде зверху вниз (рис. 5, б). Поклеточного сума цих двох квадратів (рис. 5, в) утворює магічний квадрат. Цей метод використовується і при побудові квадратів парного порядку.
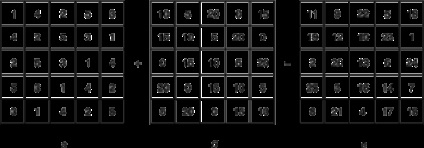
Проаналізувавши дану схему заповнення по малюнку, я прийшла до наступного алгоритму.
1. У першому квадраті розміщуємо числа від 1 до n (порядок квадрата), так, щоб на побічної діагоналі стояв середній елемент цієї послідовності.
2. Всі інші елементи маємо паралельно цій діагоналі по ламаним діагоналях. Елементи на ламаній діагоналі рівні.
3. У другому квадраті розміщуємо послідовні числа, кратні порядку квадрата, починаючи з 0, (кількість елементів одно порядку квадрата) так, щоб на головній діагоналі стояв середній елемент цієї послідовності.
4. Всі інші елементи маємо паралельно цій діагоналі по ламаним діагоналях. Елементи на ламаній діагоналі рівні.
2.3. Добудовування до симетричною
ступінчастою ромбоподібної фігури
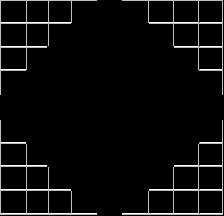

Отримана на кроці 1 фігура заповнюється по косим рядах знизу-вгору - направо цілими числами від 1 до n 2 послідовно. Результат заповнення показаний на наступному малюнку:
Глава 4. Способи заповнення магічних квадратів
порядку, кратного чотирьом
Універсальні методи складання магічних квадратів довільного парного порядку поки невідомі. Однак, розроблені індивідуальні підходи для різних окремих випадків. Нижче розглянуто метод складання магічних квадратів, порядок кратний 4. Цей метод зручно розглянути на прикладі магічного квадрата 8-го порядку з натуральних чисел від 1 до 64. Метод включає наступну послідовність кроків.
Квадрат розфарбовується в два кольори, а потім заповнюється - простежте за розстановкою послідовних чисел 1, 2, 3, 4, 5.
1. Вихідний квадрат ділиться на відповідне число квадратів порядку 4. В даному випадку таких квадратів буде 4. У кожному подквадрате закрашуються діагональні елементи (головна і побічна).
2. Інші елементи через підрядник заповнюються порядковими цілими числами в напрямку зліва -направо і зверху-вниз по зафарбовані клітинам і праворуч -налево і знизу-вгору по які зафарбовані клітинам.
3. Перехід між квітами при заповненні відбувається якщо наступна для заповнення клітина змінює колір

Глава 5. Застосування магічних квадратів.
Традиційною сферою застосування МК є талісмани. (Повний список планетних талісманів можна знайти в монографії А.Санарова «Магія талісманів. Практичний посібник»).
Наприклад, талісман Місяця має певні властивості: оберігає від корабельної аварії і хвороб, робить людину люб'язним, сприяє запобіганню поганого наміру, а так же зміцнює здоров'я. Його гравірують на сріблі в день і годину Місяця, коли Сонце або Місяць знаходиться в перших десяти градусах Рака. Магічний квадрат 9-ого порядку вписується в Дев'ятикутник (9 - число Місяця, див. Нижче) і оточується спеціальними символами.
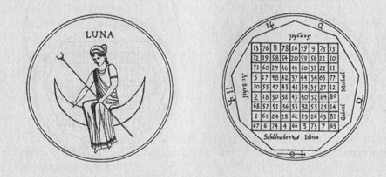
Однак, існують і магічний квадрат для стихій і знаків Зодіаку. Знайти порядок потрібного магічного квадрата допоможе Liber 777 Алістера Кроулі, яка встановлює наступні відповідності:
Тема математичних квадратів - один з традиційних розділів цікавої математики, що представляє допитливому читачеві, як красиві конструкції, так і серйозні невирішені проблеми.
У моїй роботі розглянуті питання, пов'язані з історією розвитку одного з питань математики, який обіймав уми дуже багатьох великих людей, - магічних квадратів. Незважаючи на те, що власне магічні квадрати не знайшли широкого застосування в науці і техніці, вони спонукали на заняття математикою безліч непересічних людей і сприяли розвитку інших розділів математики (теорії груп, визначників, матриць і т.д.).
Мною зроблено такі висновки:
1. Існує не так багато методів заповнення магічних квадратів
2. Зі збільшенням розмірів квадрата швидко зростає кількість можливих магічних квадратів. Так, наприклад, для 3 порядку - єдиний, для 4 - 880, для 5 - наближається до чверті мільйона.
Важко зрозуміти класичну музику без підготовки. Нелегко сприймати абстрактну живопис, не маючи уявлення про її законах. Те ж можна сказати про числових візерунках.
Дивовижна, воістину, магічна краса, що міститься в магічних квадратах, вабить до себе кращі уми людства протягом тисячоліть. Зрозуміти її не всякому дано, але один раз усвідомивши стрункість і безжальну суворість чисел, пов'язаних узами магії, можна отримати величезне задоволення.
Використані Інтернет-ресурси та література
1. Е.И Ігнатьєв «У царстві кмітливості», М. «Наука», 1979р.
2. І. Я. Депман, Н.Я. Виленкин. За сторінками підручника математики.
3. Москва. Просвітництво. 1989р.
5. Постніков M.М. «Магічні квадрати» - М. Наука, 1964 року
7. Енциклопедичний словник юного математика. М. «Педагогіка», 1989р.
Мною складено завдання на тему «Магічні квадрати» для вирішення на спецкурсі з математики.


Завдання 3. Розставити 16 букв
У квадраті, що складається з 16 клітин, розставити
16 букв (4 букви a, 4 букви b, 4 букви c, 4 букви d)
так, щоб в кожному горизонтальному і вертикальному ряду будь-яка буква зустрічалася тільки один раз.
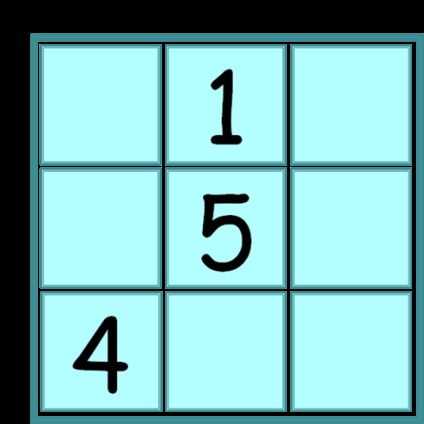
Завдання 4. Розставити 9 чисел
В квадраті складається з 9 клітин, розставити числа 1,2,3,4,5,6,7,8,9 так, щоб суми чисел, що стоять в кожному вертикальному, горизонтальному ряду, а також на будь-який діагоналі були рівні.