Мета роботи: навчитися вирішувати прикладні завдання за допомогою похідної.
Приклад виконання завдань
1. Тіло рухається прямолінійно по заданому закону.
a. Знайти миттєву швидкість тіла в момент часу секунду.
b. Знайти прискорення тіла в момент часу секунди.
c. Знайти, через скільки секунд від початку відліку миттєва швидкість тіла дорівнюватиме = 44м / с.
d. Знайти, через скільки секунд від початку відліку прискорення тіла дорівнюватиме.
a) Для знаходження швидкості обчислимо похідну першого порядку. Тоді миттєва швидкість через 1 секунду.
b) Для знаходження прискорення обчислимо другу похідну. Тоді через 2 секунди прискорення буде.
c) Для визначення часу, після закінчення якого швидкість тіла дорівнюватиме 44м / с необхідно вирішити рівняння. Отримуємо t = 2 секунди.
d) Для визначення часу, після закінчення якого прискорення тіла дорівнюватиме 22м / с 2 необхідно вирішити рівняння. Залишається знайти t.
Відзначимо, що якщо у Вашому варіанті у відповідній колонці стоїть прочерк, значить цей пункт робити не треба.
2. Скласти рівняння дотичної до графіка функції
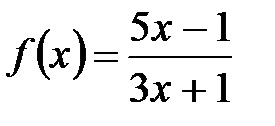
За умовою завдання x0 = 1 і f (x0) = f0 = 1. Рівняння дотичної має вигляд
.
Таким чином, залишається знайти
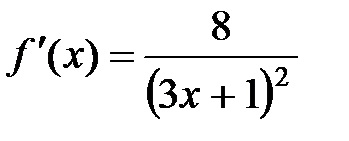
Тоді рівняння дотичної матиме вигляд
1. Тіло рухається прямолінійно по заданому закону S (t).
a. Знайти миттєву швидкість тіла в момент часу.
b. Знайти прискорення тіла в момент часу.
c. Знайти, через скільки секунд від початку відліку миттєва швидкість тіла дорівнюватиме.
d. Знайти, через скільки секунд від початку відліку прискорення тіла дорівнюватиме.
Тіло рухається прямолінійно за законом S (t)