Як показники ефективності СМО з очікуванням, крім уже відомих показників - абсолютної і відносної пропускної здатності, ймовірності відмови, середнього числа зайнятих каналів до (для багатоканальної системи) будемо розглядати також наступні:
1) - середнє число заявок в системі;
2) - середній час перебування заявки в системі;
3) - середнє число заявок в черзі (довжина черги);
4) - середній час перебування заявки в черзі;
5) - ймовірність того, що канал зайнятий (ступінь завантаження каналу).
Одноканальна система з необмеженою чергою
Є одноканальна СМО з чергою, на яку не накладені ніякі обмеження (ні по довжині черги, ні за часом очікування). Потік заявок, що надходять в СМО, має інтенсивність, а потік обслуговуванні - інтенсивність. Необхідно знайти граничні ймовірності станів і показники ефективності СМО.
Система може знаходитися в одному з станів, по числу заявок, що знаходяться в СМО: - канал вільний; - канал зайнятий (обслуговує заявку), черги немає; - канал зайнятий, одна заявка стоїть в черзі; - канал зайнятий, заявок стоять в черзі і т.д.
Граф станів СМО представлений на рис. 8.
Це процес загибелі і розмноження, але з нескінченним числом станів, в якому інтенсивність потоку заявок дорівнює, а інтенсивність потоку обслуговуванні.
Перш ніж записати формули граничних ймовірностей, необхідно бути впевненим у їх існуванні, адже в разі, коли час, черга може необмежено зростати. Доведено, що якщо, тобто середнє число приходять заявок менше середнього числа обслужених заявок (в одиницю часу), то граничні ймовірності існують. Якщо, чергу зростає до нескінченності.
Для визначення граничних ймовірностей станів скористаємося формулами (16), (17) для процесу загибелі і розмноження (тут ми допускаємо відому нестрогість, так як раніше ці формули були отримані для випадку кінцевого числа станів системи). отримаємо:
Приклад 8. У порту є один причал для розвантаження судів. Інтенсивність потоку судів рівна 0,4 (судів в добу). Середній час розвантаження одного судна становить 2 доби. Передбачається, що черга може бути необмеженої довжини. Знайти показники ефективності роботи причалу, а також ймовірність того, що очікують розвантаження не більше ніж 2 судна.
Рішення. Маємо. Так як, то чергу на розвантаження не може нескінченно зростати і граничні ймовірності існують. Знайдемо їх.
Імовірність того, що причал вільний, по (33), а ймовірність того, що він зайнятий,. За формулою (34) ймовірності того, що біля причалу перебувають 1, 2, 3 судна (тобто очікують розвантаження 0, 1, 2 судна), рівні
Імовірність того, що очікують розвантаження не більше ніж 2 судна, дорівнює
За формулою (40) середнє число суден, які очікують розвантаження, середній час очікування розвантаження за формулою (42) (добу).
За формулою (36) середнє число суден, що знаходяться біля причалу, (добу) (або простіше по (37) (добу), а середній час перебування судна біля причалу за формулою (41) (добу).
Очевидно, що ефективність розвантаження судів невисока. Для її підвищення необхідно зменшення середнього часу розвантаження судна або збільшення числа причалів.
Багатоканальна СМО з необмеженою чергою
Розглянемо задачу. Є n-канальна СМО з необмеженою чергою. Потік заявок, що надходять в СМО, має інтенсивність, а потік обслуговуванні - інтенсивність. Необхідно знайти граничні ймовірності станів СМО і показники її ефективності.
Система може знаходитися в одному з станів нумерованих по числу заявок, що знаходяться в СМО: - в системі немає заявок (всі канали вільні); - зайнятий один канал, інші вільні; - зайняті два канали, інші вільні; - зайнято каналів, інші вільні; - зайняті всі каналів (черги немає); - зайняті всі каналів, в черзі одна заявка; - зайняті всі каналів, заявок стоїть у черзі, і т.д.
Граф станів системи показаний на рис. 9. Звернемо увагу на те, що на відміну від попередньої СМО, інтенсивність потоку обслуговуванні (переводить систему з одного стану в інший справа наліво) не залишається постійною, а в міру збільшення числа заявок в СМО від 0 до збільшується від величини до, так як відповідно збільшується число каналів обслуговування. При числі заявок в СМО більшому, ніж, інтенсивність потоку обслуговуванні зберігається рівною.
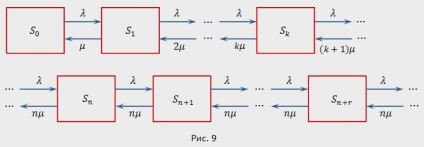
Можна показати, що при граничні ймовірності існують. Якщо, чергу зростає до нескінченності. Використовуючи формули (16) і (17) для процесу загибелі і розмноження, можна отримати наступні формули для граничних ймовірностей станів n-канальної СМО з необмеженою чергою
Середній час перебування заявки в черзі і середній час перебування заявки в системі, як і раніше, знаходяться за формулами Літтла (42) і (41).
Зауваження. Для СМО з необмеженою чергою при будь-яка заявка, що прийшла в систему, буде обслужена, тобто ймовірність відмови, відносна пропускна здатність, а абсолютна пропускна здатність дорівнює інтенсивності вхідного потоку заявок, тобто .
Приклад 9. У універсамі до вузла розрахунку надходить потік покупців з інтенсивністю чол. в годину. Середня тривалість обслуговування контролером-касиром одного покупця хв. визначити:
а. Мінімальна кількість контролерів-касирів, при якому черга не буде рости до безкінечності, і відповідні характеристики обслуговування при.
в. Імовірність того, що в черзі буде не більше трьох покупців.
Рішення. а. За умовою (1 / ч) (1 / хв.). За формулою (24). Черга не буде зростати до нескінченності за умови, тобто при \ rho = 2, \! 7 "src =" http://www.bourabai.kz/cm/waiting_sys/mathtex(82).gif ">. Таким чином, мінімальна кількість контролерів-касирів.
Знайдемо характеристики обслуговування СМО при.
Імовірність того, що в вузлі розрахунку відсутні покупці, по формулі (45)
тобто в середньому 2,5% часу контролери-касири будуть простоювати.
Імовірність того, що в вузлі розрахунку буде чергу, по (48)
Середнє число покупців, що знаходяться в черзі, по (50)
Середній час на очікування в черзі і покупку квитків дорівнює відповідно (за формулами (42) і (41)):
За другим варіантом маємо дві одноканальні СМО (два спеціалізованих віконця); на кожну надходить потік заявок з інтенсивністю. Як і раніше, граничні ймовірності існують. За формулами (40), (36), (42), (41)
Отже, за другим варіантом збільшилися і довжина черги, і середній час очікування в ній і в цілому на покупку квитків. Така відмінність пояснюється тим, що в першому варіанті (двоканальна СМО) менше середня частка часу, яку простоює кожен з двох касирів: якщо він не зайнятий обслуговуванням пасажира, який купує квиток в пункт, він може зайнятися обслуговуванням пасажира, який купує квиток в пункт, і навпаки . У другому варіанті такий взаємозамінності немає.
Можна помітити, що середній час на покупку квитків за другим варіантом збільшилася більш ніж в 2 рази. Таке значне збільшення пов'язане з тим, що СМО працює на межі своїх можливостей: досить незначно збільшити середній час обслуговування, тобто зменшити, і перевершить 1, тобто чергу почне необмежено зростати.
б. Вище було отримано, що за першим варіантом продажу квитків при середньому часу обслуговування одного пасажира (хв) середнє час на покупку квитків складе (хв). За умовою для другого варіанту продажу, або з урахуванням (36) і (41):.
Вважаючи, отримаємо, звідки знайдемо або (хв).
Отже, середні витрати часу на купівлю квитків за другим варіантом продажу зменшаться, якщо середній час обслуговування одного пасажира зменшиться більш ніж на 0,17 хв, або більш ніж на 8,5%.
СМО з обмеженою чергою
СМО з обмеженою чергою відрізняються від розглянутих вище завдань лише тим, що число заявок в черзі обмежена (не може перевищувати деякого заданого). Якщо нова заявка надходить в момент, коли всі місця в черзі зайняті, вона залишає СМО необслуженной, тобто отримує відмову.
Очевидно: для обчислення граничних ймовірностей станів і показників ефективності таких СМО може бути використаний той же підхід, що й вище, з тією різницею, що підсумовувати треба не нескінченну прогресію (як, наприклад, ми робили при виведенні формули (33)), а кінцеву . Відповідні формули зведемо в табл. 3.
Середній час перебування заявки в черзі і в системі, як і раніше, визначаємо за формулами Літтла (44) і (43).
Приклад 11. За умовою прикладу 8 знайти показники ефективності роботи причалу. Відомо, що приходить судно залишає причал (без розвантаження), якщо в черзі на розвантаження варто більше 3 судів.
Рішення. За умовою . Використовуємо формули, наведені в другій графі табл. 3.
Імовірність того, що причал вільний:
Імовірність того, що приходить судно покине причал без розвантаження:
Середнє число суден, що знаходяться біля причалу, а середній час перебування судна біля причалу по (41):
СМО з обмеженим часом очікування
На практиці часто зустрічаються СМО з так званими "нетерплячими" заявками. Такі заявки можуть піти з черги, якщо час очікування перевищує деяку величину. Зокрема, такого роду заявки виникають в різних технологічних системах, в яких затримка з початком обслуговування може призвести до втрати якості продукції, в системах оперативного управління, коли термінові повідомлення втрачають цінність (або навіть сенс), якщо вони не надходять на обслуговування протягом певного часу.
У найпростіших математичних моделях таких систем передбачається, що заявка може перебувати в черзі випадкове час, розподілене по показовому закону з деяким параметром, тобто можна умовно вважати, що кожна заявка, що стоїть в черзі на обслуговування, може покинути систему з інтенсивністю.
Відповідні показники ефективності СМО з обмеженим часом виходять на базі результатів, отриманих для процесу загибелі і розмноження.
На закінчення відзначимо, що на практиці часто зустрічаються замкнуті системи обслуговування. у яких вхідний потік заявок істотно залежить від стану самої СМО. Як приклад можна навести ситуацію, коли на ремонтну базу надходять з місць експлуатації деякі машини: зрозуміло, що чим більше машин знаходиться в стані ремонту, тим менше їх продовжує експлуатуватися і тим менше інтенсивність потоку тих, хто влаштовується на ремонт машин. Для замкнутих СМО характерним є обмежене число джерел заявок, причому кожне джерело "блокується" на час обслуговування його заявки (тобто він не видає нових заявок). У подібних системах при кінцевому числі станів СМО граничні ймовірності будуть існувати при будь-яких значеннях інтенсивностей потоків заявок і обслуговуванні. Вони можуть бути обчислені, якщо знову звернутися до процесу загибелі і розмноження.
Чи знаєте Ви, що алгоритм - це набір інструкцій, що описують порядок дій виконавця для досягнення результату рішення задачі за кінцеве число дій. У старій трактуванні замість слова "порядок" використовувалося слово "послідовність", але в міру розвитку паралельності в роботі комп'ютерів слово "послідовність" стали замінювати більш загальним словом "порядок". Це пов'язано з тим, що робота якихось інструкцій алгоритму може бути залежна від інших інструкцій або результатів їх роботи. Таким чином, деякі інструкції повинні виконуватися строго після завершення роботи інструкцій, від яких вони залежать. Незалежні інструкції або інструкції, що стали незалежними через завершення роботи інструкцій, від яких вони залежать, можуть виконуватися в довільному порядку, паралельно або одночасно, якщо це дозволяють використовувані процесор і операційна система.
НОВИНИ ФОРУМУ
Лицарі теорії ефіру