Почнемо стискати газ, підтримуючи його температуру постійною, з якою-небудь точки А. Гілка ізотермиАВ (на обох малюнках) відповідає стисненню газу при низькому тиску. Властивості газу на участкеАВ дуже близькі до властивостей ідеального газу. При досягненні деякого давленіяР0 поведінку газу різко змінюється.
Газ продовжуємо стискати, його обсяг зменшується, а тиск залишається одним і тим же (рис. 16.3), рівним Р0. УчастокВС наексперіментальной изотерме відповідає процесу скраплення газу, тобто на участкеВС газ перетворюється в рідину (ВС - лінія конденсації пари). У цій області речовина існує одночасно в двох фазах: рідина - одна фаза, і друга фаза - газ, який в даному випадку є насиченою парою по відношенню до рідини. Тиск насиченої пари залежить тільки від температури, але не залежить від обсягу. Тому давленіеР0 не змінюється до тих пір, поки весь пар при даній температурі, не перейде в рідину. ДавленіеP0 називаетсяупругостью насичених парів при даній температуреТ. У точці все речовина ще було в газоподібному стані, в точці С все речовина знаходиться вже в рідкому стані.
Гілка ізотерми СД (на обох ізотермах) характеризує процес стиснення рідини. Рідини мають малу сжимаемостью, тому кріваяСД круто йде вгору.
Ділянка ВЕтеоретіческой ізотерми Ван-дер-Ваальса можна отримати на досвіді. УчастокВЕ характерізуетпересищенний пар. тобто пар, щільність якого більше щільності насиченої пари при даній температурі. Стан пересичені пара - малоустойчивое стан. Пар легко конденсується, частково переходить в рідину, а залишився пар тоді буде вже насиченою парою.
Ділянка СFтеоретіческой ізотерми Ван-дер-Ваальса також можна отримати експериментально. Він характеризує малоустойчивое состояніерастянутой рідини. тобто рідини з меншою щільністю, ніж їй належить мати при даній температурі. Така рідина виходить, якщо її особливо ретельно очистити від всяких домішок.
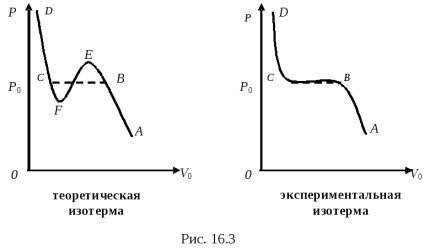
Ділянка FЕтеоретіческой ізотерми Ван-дер-Ваальса експериментально отримати не можна.
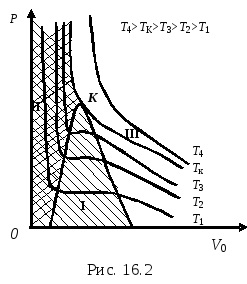
Кожна експериментальна ізотерма відповідає однієї будь-якої температурі Т = const. З підвищенням температури прямолінійні ділянки відповідних ізотерм стають все вже і при якійсь температуреТк точки ІС. обмежують прямолінійний ділянку, зіллються в одну точкуК. Ізотерма, на якій лінія конденсації зображується у вигляді точки, є критичною ізотермою. Температура, що відповідає критичній изотерме - критична температураTк. Ізотерма, відповідна критичної температуреТк. має тільки точку перегібаК. Дотична до точкек паралельна осі абсцис. Ізотерми при температурах вишеТк не мають ні максимумів, ні мінімумів, ні прямолінійних ділянок і близькі до ізотермам ідеального газу.
Точка К називається критичною точкой.Тк. відповідні ейPк іVк називаються критичними температурою, тиском і об'ємом соответственно.Крітіческой температуройТкназивается температура, при якій зникає відмінність між рідким і газоподібним станом речовини. Для різних речовин критична температураТк різна. Стан речовини при критичній температурі називається критичним станом речовини. У цьому стані речовина набуває особливі властивості, наприклад, зникають сили зчеплення між молекулами, речовина не має поверхневого натягу і т.п.
При температурах нижче критичної речовина може існувати в залежності від тиску або в рідкому, або в газоподібному стані, або в двофазному стані (рідина і її пар одночасно).
При температурах вище критичної температури речовина може існувати тільки в газоподібному стані і ніяким стисненням не може бути переведено в рідкий стан. Газ спочатку треба охолодити до ТТк. і тільки потім стискати.
Критичного стану речовини відповідає єдина точка критичної ізотерми - точка, в яку перетворилася лінія конденсації. Ця точка називається критичною. Параметри речовини в критичній точці називають критичними параметрами. Для їх визначення необхідно встановити положення критичної точки на координатній площині P, V.
Будь-яка ізотерма Ван-дер-Ваальса, в тому числі і критична, описується рівнянням
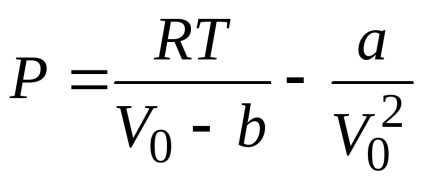
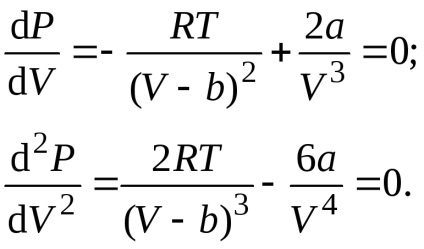
Вирішуючи рівняння спільно, знайдемо значення критичних параметрів:
де а, b - константи з рівняння Ван-дер-Ваальса, що описує стан даного реального газу, R - універсальна газова стала. На малюнку областьI (заштрихована) - це область двофазного стану речовини, областьII (подвійна штриховка) - це область рідкого стану, областьIII (НЕ заштриховано) - це область газоподібного стану.