Дмитро Шахов, фрілансер, м.Москва
Фрактали привертають увагу, заворожують, гіпнотизують. Однак багато хто вважає, що такі зображення - просто візерунки, які хороші лише на екрані монітора або в якості прикладних допоміжних засобів для оформлення різної поліграфічної продукції. При цьому мало хто здогадується, що простота ця тільки уявна. Насправді фрактальная графіка досить складна і є результатом злиття математики і мистецтва. Сьогодні фрактали - один з найперспективніших, швидко розвиваються видів комп'ютерної графіки.
Перш ніж перейти до розгляду фрактальної графіки, розглянемо, в чому суть комп'ютерної, або «машинної», графіки, а також загальноприйняту класифікацію комп'ютерної графіки (Computer Graphics, CG). Це поняття з'явилося відносно недавно, в 60-х роках минулого століття, коли були винайдені електронні обчислювальні пристрої. Термін «комп'ютерна графіка» трактується в різних джерелах по-різному. Деякі визначають його як область інформатики, що займається питаннями отримання різних зображень (малюнків, креслень, мультиплікації) на комп'ютері. Комп'ютерна графіка охоплює всі види та форми представлення зображень, доступні для людського сприйняття на екрані монітора або в вигляді копії на зовнішньому носії (папері, тканині, кіноплівці і т.п.). В інших джерелах комп'ютерна графіка називається спеціальною областю інформатики, що вивчає методи і засоби створення та обробки зображень за допомогою программноаппаратних обчислювальних комплексів.



У широкому сенсі слова комп'ютерна графіка - це все, для чого використовується візуальна, образна середу відображення на моніторі. Якщо звузити поняття до практичного використання, то під комп'ютерною графікою можна мати на увазі процес створення, обробки і виведення різного роду зображень за допомогою комп'ютера.
Залежно від способу формування зображень комп'ютерна графіка ділиться на растрову, векторну і фрактальну (рис. 1).
Основним і найменшим елементом растрового зображення є точка. Коли зображення перебуває в програмному середовищі на екрані, вона називається пикселом. Кожен піксель растрового зображення має дві характеристики: розміщення і колір. Чим більше кількість пікселів і менше їх розміри, тим краще виглядає зображення. Великі обсяги даних - це основна проблема при використанні растрових зображень. Другий недолік растрових зображень пов'язаний з неможливістю їх збільшення для розгляду деталей. Оскільки зображення складається з точок, збільшення зображення призводить до того, що ці точки стають більшими і нагадують мозаїку, а отже, додаткових деталей в цьому випадку розглянути не вдається. Більш того, збільшення точок растру візуально спотворює зображення і робить його зернистим. Цей ефект називається пікселізацією.

Мал. 1. Типи комп'ютерної графіки: а - растрова; б - векторна; в - фрактальна
У векторній графіці основним елементом зображення є лінія (не важливо, пряма або крива). Зрозуміло, в растровій графіці теж існують лінії, але там вони розглядаються як комбінації точок. Для кожної точки лінії в растровій графіці відводиться одна або кілька осередків пам'яті (чим більше кольорів можуть мати точки, тим більше клітинок їм виділяється). Відповідно, чим довше растрова лінія, тим більше пам'яті вона займає. У векторній графіці об'єм пам'яті, займаний лінією, не залежить від розмірів лінії, оскільки лінія представляється у вигляді формули, а точніше, у вигляді декількох параметрів. Що б ми не робили з цією лінією, міняються тільки її параметри, що зберігаються в осередках пам'яті. Кількість же осередків для будь-якої лінії залишається незмінним.

Мал. 2. Приклад фрактальности в природі - капуста Романеско
Зображення у векторному форматі легко редагується: його можна без втрат масштабувати, повертати, деформувати. Імітація тривимірності в векторній графіці теж простіше, ніж в растровій. Справа в тому, що кожне перетворення фактично виконується так: старе зображення (або фрагмент) стирається, а замість нього будується нове. Математичний опис векторного малюнка залишається колишнім - змінюються тільки значення деяких змінних, наприклад коефіцієнтів.
Фрактальна графіка відносно молода в порівнянні з растровою і векторною графікою. Основою фрактальної графіки є фрактальна геометрія, що дозволяє математично описувати різні види неоднорідностей, що зустрічаються в природі. Поняття «фрактал», «фрактальная геометрія» і «фрактальная графіка» з'явилися в кінці 1970-х. Слово «фрактал» утворено від латинського fractus і означає «складається з фрагментів». Воно було запропоновано математиком Бенуа Мандельброт в 1975 році для позначення нерегулярних, але самоподібних структур. Народження фрактальної геометрії прийнято пов'язувати з виходом в 1977 році книги «The Fractal Geometry of Nature» Бенуа Мандельброта. Визначення фрактала, дане Мандельброт: фракталом називається структура, що складається з частин, які в якомусь сенсі подібні цілому. Самоподібність - одне з основних властивостей фракталів. Таким чином, фрактальна графіка - це вид комп'ютерної графіки, в якій в тій чи іншій мірі використовуються самоподібні структури (простіше кажучи, фрактали). Далі ми поговоримо про те, що ж таке самоподоба і де в природі зустрічаються фрактали.
Що мається на увазі під самоподібності? Капуста Романеско з Італії - найхарактерніший приклад фрактального об'єкта в природі. Капустяні нирки у неї наростають у вигляді якоїсь спіралі (рис. 2), яка називається логарифмічною, а число капустяних нирок збігається з числом Фібоначчі. Числа Фібоначчі - це елементи числової послідовності 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1 597, 2 584, 4181, 6765, 10946 ..., в якій кожне наступне число дорівнює сумі двох попередніх чисел. Свою назву вони отримали на честь середньовічного математика Леонардо Пізанського (відомого як Фібоначчі). Кожна частина елементів капусти Романеско має ту ж форму, що і весь качан. Це властивість повторюється з регулярністю в різних масштабах. По суті ця капуста є природним фракталом. Тобто як би ми не збільшували фрактал, після кожного кроку ми побачимо ту ж форму, що характерна для даного фрактала в цілому. Таким чином, з фракталами тісно пов'язані ще два поняття - ітерація і рекурсія. Рекурсія - процес повторення елементів самоподібним чином. Ітерація - спрощено кажучи - повторне застосування якої-небудь математичної операції.
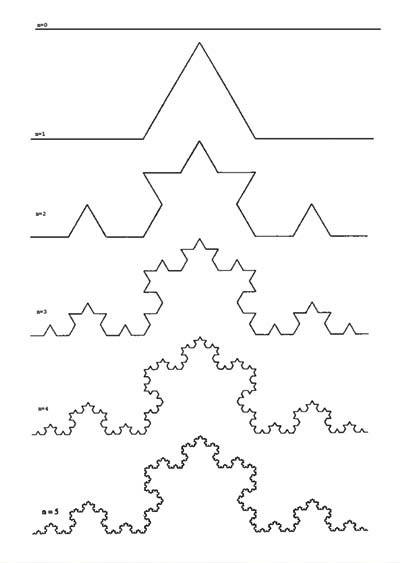
Мал. 3. Рекурсія кривої Коха
Насправді фрактальні властивості має дуже велику кількість природних об'єктів - просто мало хто про це замислюється. Ви можете милуватися хмарами на небі, що набігають хвилями прибою, ходити по лісі - і навіть не підозрювати, що в основі цієї краси лежить математика! Так Так! Дослідження фрактальних властивостей природних об'єктів почав проводити ще Бенуа Мандельброт. Виявляється, незважаючи на всю складність природних об'єктів, багато з них в принципі описуються досить простими математичними формулами. Хоча в чистому вигляді фрактали в природі не існують. Те, що ми спостерігаємо, - це так звані стохастичні фрактали. Тобто такі фрактали, які виходять в тому випадку, якщо в ітераційне процесі випадковим чином змінювати які-небудь його параметри. «Чистий» фрактал можна наближати до нескінченності, оскільки він володіє нескінченною рекурсією, а ось про стохастичних фракталах цього сказати не можна.
Слід зазначити, що слово «фрактал» не є математичним терміном і не має загальноприйнятого суворого математичного визначення. Воно може вживатися, коли розглянута фігура володіє какимилибо з наступних властивостей:
- має нетривіальну структуру у всіх масштабах - цим фрактал відрізняється від регулярних фігур (таких як коло, еліпс, графік гладкої функції): якщо ми розглянемо невеликий фрагмент регулярної фігури в дуже великому масштабі, то він буде схожий на фрагмент прямої. Для фрактала збільшення масштабу не веде до спрощення структури, тому на всіх шкалах ми побачимо однаково складну картину;
- є самоподобной або наближено самоподобной;
- має дробову метричну розмірність або метричну розмірність, що перевершує топологічну.
Крім того, для побудови фрактала необхідно враховувати початковий стан і описує його формулу - так зване початкове безліч, яке пропускається через якийсь механізм, що викликає його відображення і додає відображене безліч до вихідного. Цей процес і називається итерацией. Таким чином, після декількох подібних щодо простих операцій виходить вельми складне зображення. У процесі отримання фрактала важливі два моменти: вихідне безліч і механізм перетворення. Залежно від алгоритму побудови фрактали діляться на лінійні і нелінійні.
Алгоритми побудови лінійних фракталів визначаються лінійними функціями. У них самоподоба присутній в найпростішому варіанті: будь-яка частина повторює ціле.
Нелінійні фрактали задаються нелінійної функцією зростання, тобто рівняннями в ступеня вище першої. У них самоподоба буде більш складним: будь-яка частина є вже не точною, а деформованої копією цілого.
Один з найпростіших прикладів лінійного фрактала - крива Коха (1904 рік, німецький математик Хельга фон Кох).
Існує проста рекурсивна процедура (отримання самоподібних частин фрактала) формування фрактальних кривих на площині. Задамо довільну ламану з кінцевим числом ланок, звану генератором. Далі замінимо в ній кожен відрізок генератором (точніше, ламаної, подібної генератору). У вийшла ламаної знову замінимо кожен відрізок генератором. Продовжуючи до нескінченності, в межі отримаємо фрактальну криву. На рис. 3 наведено кілька кроків цієї процедури для кривої Коха.
Одним з перших нелінійні фрактали описав французький математик Гастон Жюліа ще в 1918 році. Але в його роботі були відсутні зображення досліджених їм множин і термін «фрактал».
У наш час комп'ютери дозволили отримати зображення множин Жюліа (рис. 4а), які разом з множинами Мандельброта (рис. 4б) є нині найвідомішими квадратичними фрактальними структурами.


Мал. 4. Зображення множин Жюліа (а) і Мандельброта (б)
Обидва типи фракталів виникають в результаті реалізації на комплексній площині самого простого нелінійного алгоритму.
Тут в основу методу побудови зображень покладено принцип спадкування від так званих батьків геометричних властивостей об'ектовнаследніков. Побудова фрактального малюнка здійснюється за какомулібо алгоритму або шляхом автоматичної генерації зображень за допомогою обчислень по конкретним формулами. Зміни значень в алгоритмах або коефіцієнтів у формулах призводить до модифікації цих зображень. Головною перевагою фрактальної графіки є те, що в файлі фрактального зображення зберігаються тільки алгоритми і формули.
Фрактал - об'єкт, окремі елементи якого успадковують властивості батьківських структур. Оскільки більш детальний опис елементів меншого масштабу відбувається по простому алгоритму, описати такий об'єкт можна всього декількома математичними рівняннями.
Фрактали дозволяють описувати цілі класи зображень, для детального опису яких потрібно відносно мало пам'яті. У той же час фрактали слабо застосовні до зображень поза цих класів.
Програмні засоби для роботи з фрактальною графікою призначені для автоматичної генерації зображень шляхом математичних розрахунків. Саме тому фрактальная графіка не визнається ні комп'ютерними, ні звичайними художниками через те, що нібито тут за людину все робить програма. Насправді процес роботи з графікою фрактальної хоч і автоматизований, але, тим не менш, повністю творчий: комбінуючи формули і змінюючи змінні, можна добиватися дивовижних результатів і втілювати в життя найсміливіші художні задуми. Створення фрактальної художньої композиції полягає не в малюванні або оформленні, а в програмуванні.
Змінюючи і комбінуючи забарвлення фрактальних фігур, можна моделювати образи живої та неживої природи (наприклад, гілки дерева або сніжинки), а також складати з отриманих фігур «фрактальную» композицію. Фрактальна графіка, так само як векторна і тривимірна, є обчислюється. Її головна відмінність в тому, що зображення будується за рівнянням або системі рівнянь. Тому для виконання всіх обчислень в пам'яті комп'ютера нічого, крім формули, зберігати не потрібно.


Мал. 5. Зображення, отримані за допомогою фракталогенераторов
Тільки змінивши коефіцієнти рівняння, можна отримати зовсім інше зображення. Ця ідея знайшла застосування в комп'ютерній графіці завдяки компактності математичного апарату, необхідного для її реалізації. Так, за допомогою декількох математичних коефіцієнтів можна задати лінії і поверхні дуже складної форми.
У машинній графіці фрактальная геометрія незамінна при генерації штучних хмар, гір, поверхні моря. Фактично, завдяки фрактальної графіку знайдений спосіб ефективної реалізації складних неевклідових об'єктів, образи яких дуже схожі на природні. Власне, тому цій статті і дано таку назву. Багато природні об'єкти мають фрактальні властивості, тому їх легко створювати на комп'ютері за допомогою фрактальної графіки. Наприклад, при розробці комп'ютерної гри немає потреби кожного разу заново малювати ліс, гори, хмари і т.д. Ці об'єкти мають самоподібності, а отже, можуть бути легко згенеровані програмними засобами на основі математичних формул. Додаючи або змінюючи деякі параметри вихідної формули, можна домогтися дивного різноманітності одержуваних природних об'єктів. Фрактали на екрані комп'ютера - це візерунки, побудовані самим ПК за заданою програмою. Крім фрактальної живопису існують фрактальні анімація і музика.
На закінчення хотілося б відзначити наступне: фрактальна графіка - одне з найбільш незвичайних і перспективних напрямків в комп'ютерній графіці. Результати, які можна отримати з її допомогою, вражають уяву навіть найдосвідченіших цінителів комп'ютерного мистецтва. Так, зображення, що створюються за допомогою программфракталогенераторов, часом містять абсолютно фантастичні і незвичайні пейзажі (рис. 5), які навіть не снилися художнікамсюрреалістам. І навпаки, за допомогою фрактальної графіки можна з дивовижною точністю зобразити те, що ми бачимо в навколишньому світі. Воістину світ фракталів дивовижний!
Оздоблення друкованої продукції: лакування і ламінування
Обробкою друкованої продукції називають найрізноманітніші процеси, спрямовані на поліпшення її властивостей: товарного вигляду, зносостійкості, водостійкості і т.п.
Складові хорошою газети: дизайн, верстка, контент
Існує гарна традиція - коли треба підкреслити, що раніше було добре, а зараз все не так, то починають порівняння чого-небудь з 1914 роком або з кращими роками радянського періоду
Що потрібно знати про трафаретних фарбах
Трафаретний друк, або, як її часто називають, шовкографія, - це вид друку, що дозволяє наносити фарбу самої різної товщини на матеріали з усілякою текстурою
Популярні статті
Видалення ефекту червоних очей в Adobe Photoshop
При недостатньому освітленні в момент зйомки дуже часто доводиться використовувати спалах. Якщо об'єктами зйомки є люди або тварини, то в темряві їх зіниці розширюються і відображають спалах фотоапарата. Що з'явилося відображення називається ефектом червоних очей
CorelDRAW: розміщення тексту вздовж кривої
У цій статті наведені приклади розміщення фігурного тексту уздовж розімкнутої і замкнутої траєкторії. Розглянуто можливі настройки його положення відносно кривої, а також розказано, як відокремити текст від траєкторії
Нормативні вимоги до етикеток
Етикетка - це переважно друкована продукція, що містить текстову або графічну інформацію і виконана у вигляді наклейки або бирки на будь-який продукт виробництва