Для кожної квадратної матриці А вводиться число | А |, яке називають її визначником. Іноді його ще позначають буквой.
Це поняття є важливим для вирішення ряду практичних завдань. Визначимо його через спосіб обчислення.
Для матриці А першого порядку її визначником називають її єдиний елемент | А | = 1 = а11.
Для матриці А другого порядку її визначником називають число, яке обчислюють за формулою | А | = 2 = а11 * а22 - а21 * а12
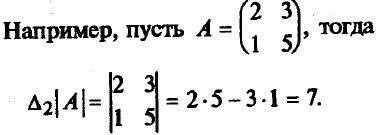
Для матриці А третього порядку її визначником називають число, яке обчислюють за формулою
Воно являє алгебраїчну суму, що складається з 6 доданків, в кожне з яких входить рівно по одному елементу з кожного рядка і кожного стовпця матриці. Для запам'ятовування формули визначника прийнято користуватися так званим правилом трикутників або правилом Сарруса (рисунок 6.1).

Малюнок 6.1 - Правило трикутників
На малюнку 6.1 схема зліва показує, яким чином вибирати елементи для доданків зі знаком «плюс», - вони знаходяться на головній діагоналі і в вершинах рівнобедрених трикутників, основи яких їй паралельні. Схема зліва використовується для доданків зі знаком «мінус»; на ній замість головної діагоналі береться так звана побічна.
Визначники вищих порядків обчислюють рекурентним способом, тобто визначник четвертого порядку через визначник третього порядку, визначник п'ятого порядку через визначник четвертого порядку і т.д. Для опису цього способу необхідно ввести поняття мінору і алгебраїчного доповнення елемента матриці (відразу ж відзначимо, що сам спосіб, який буде розглянуто далі, підходить і для визначників третього і другого порядку).
Мінором Мij елемента аij матриці n-го порядку називають визначник матриці (n-1) -го порядку, отриманої з матриці А викреслюванням i-го рядка іj-го стовпця.
Кожна матриця n-го порядку має n 2 миноров (n-1) -го порядку.
Алгебраїчним доповненням Aij елемента аij матриці n-го порядку називають його мінор, взятий зі знаком (-1) (i + j):
З визначення випливає, що Aij = Мij. якщо сума номерів рядка і стовпця парна, іAij = -Мij. якщо вона непарна.
Наприклад, якщо
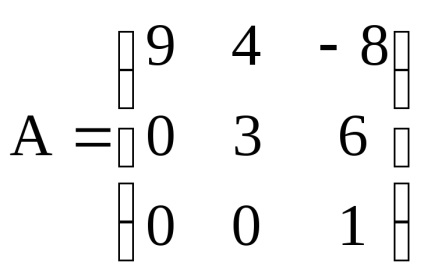
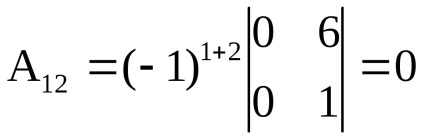
Спосіб обчислення визначника складається в наступному: визначник квадратної матриці дорівнює сумі добутків елементів будь-якого рядка (стовпця) на їх алгебраїчні доповнення:
(Розкладання по елементамi-го рядка;
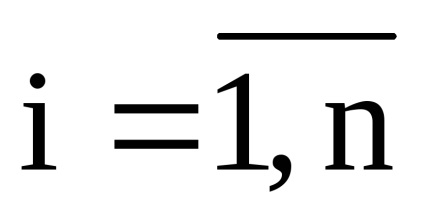
(Розкладання по елементамj-го стовпця;
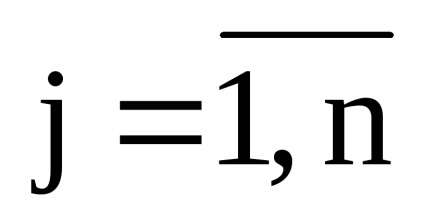

Відзначимо, що і в загальному випадку визначник трикутної матриці дорівнює добутку елементів головної діагоналі.
Сформулюємо основні властивості визначників.
1. Якщо будь-який рядок або стовпець матриці складається з одних нулів, то визначник дорівнює 0 (випливає з способу розрахунку).
2. Якщо всі елементи якого-небудь рядка (стовпчика) матриці помножити на одне і те ж число, то і її визначник множиться на це число (також випливає з способу розрахунку - на розрахунок алгебраїчних доповнень загальний множник не впливає, а все решта складові помножені саме на це число).
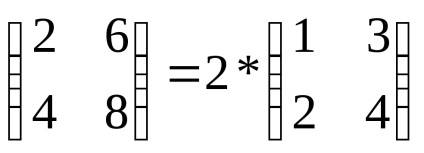
Зауваження: за знак визначника можна виносити загальний множник саме рядки або стовпці (на відміну від матриці, за знак якої можна виносити загальний множник всіх її елементів). Наприклад,, але
3. При транспонировании матриці її визначник не змінюється: | А Т | = | А | (Доказ проводити не будемо).
4. При перестановці місцями двох рядків (стовпців) матриці її визначник змінює знак на протилежний.
Для доказу цього властивості спочатку припустимо, що переставлені дві сусідні рядки матриці: i-я і (i + 1) -я. Для розрахунку визначника вихідної матриці здійснимо розкладання по i-му рядку, а для визначника нової матриці (з переставленими рядками) - по (i + 1) -й (яка в ній така ж, тобто поелементно збігається). Тоді при розрахунку другого визначника кожне алгебраїчне доповнення матиме протилежний знак, так як (-1) буде зводитися не на щабель (i + j), а в ступінь (i + 1 + j), а в іншому формули відрізнятися не будуть. Таким чином, знак визначника зміниться на протилежний.
Тепер припустимо, що переставлені не сусідньої, а дві довільні рядки, наприклад, i-я і (i + t) -я. Таку перестановку можна уявити як послідовне смещеніеi-го рядка наtстрок вниз, а (i + t) -го рядка - на (t-1) рядків вгору 1. При цьому знак визначника зміниться (t + t- 1) = 2t- 1 число раз, тобто непарне число раз. Отже, в кінцевому підсумку він зміниться на протилежний.
Аналогічні міркування можна поміняти для стовпців.
5. Якщо матриця містить дві однакові рядки (стовпці), то її визначник дорівнює 0.
Справді, якщо однакові рядки (стовпці) переставити місцями, то буде отримана та ж сама матриця з тим же самим визначників. З іншого боку, за попереднім властивості він повинен поміняти знак, тобто = - = 0.
6. Якщо елементи двох рядків (стовпців) матриці пропорційні, то визначник дорівнює 0.
Це властивість грунтується на попередньому властивості і винесення за дужку загального множника (після винесення за дужки коефіцієнта пропорційності в матриці будуть однакові рядки або стовпці, і в результаті цей коефіцієнт буде множитися на нуль).
7. Сума добутків елементів будь-якого рядка (стовпця) матриці на алгебраїчні доповнення елементів іншого рядка (стовпця) тієї ж матриці завжди дорівнює 0:
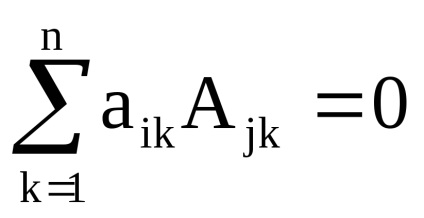
Щоб довести це властивість, досить замінити в матриці А j-й рядок наi-ю. В отриманій матриці буде дві однакові рядки, тому її визначник дорівнює 0. З іншого боку, його можна обчислити розкладанням по елементамj-го рядка:
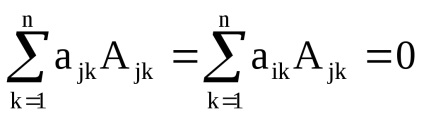
8. Визначник матриці не змінюється, якщо до елементів рядка або стовпця матриці додати елементи іншого рядка (стовпця), помножені на одне і теж число.
Справді, нехай до елементів i-го рядка додають елементиj-го рядка, помножені на. Тоді елементи новойi-го рядка візьмуть вид (aik + ajk, k). Обчислимо визначник нової матриці розкладанням за елементами i-му рядку (відзначимо, що алгебраїчні доповнення її елементів при цьому не зміняться):
Ми отримали, що цей визначник не відрізняється від визначника вихідної матриці.
9. Визначник твори матриць дорівнює добутку їх визначників: | АВ | = | А | * | В | (Доказ проводити не будемо).
Розглянуті вище властивості визначників використовують для спрощення їх обчислення. Зазвичай намагаються перетворити матрицю до такого виду, щоб будь-якої стовпець або рядок містили якомога більше нулів. Після цього визначник легко знайти розкладанням по цьому рядку або стовпцю.


