Для вирішення завдань максимізації можна використовувати два підходи.
Подход1. Перетворення завдання максимізації в еквівалентну задачу мінімізації шляхом множення цільової функції на -1 і подальшого застосування симплекс-методу до задачі мінімізації.
Підхід 2. Як показано вище, відносні оцінки в рядку pj представляють зміна цільової функції f при зменшенні небазисной змінної на одиницю. Негативний коефіцієнт в рядку pj вказує на зменшення f при збільшенні відповідної небазисной змінної.
Отже, для задач максимізації в базис повинні вводиться небазисних змінні xj з позитивними pj. оскільки вони покращують цільову функцію. Якщо всі коефіцієнти в рядку pj негативні або дорівнюють нулю, поточний рішення оптимальне.
Приклад 6.9. Вирішити симплекс - методом задачу:
Рішення. За допомогою додаткових невід'ємних змінних перейдемо до системи рівнянь. В даному випадку всі додаткові змінні вводяться зі знаком «+», так як всі нерівності мають вигляд «».
Отримаємо систему обмежень у вигляді:
І т е р а ц і я 1.
Вважаючи в равенствах (6.37) вільні змінні x1. x2 рівними нулю, знаходимо. . . . тобто базисне рішення х 0 = (0; 0; 18; 16; 5; 21). Так як всі базисні змінні в х 0 позитивні, дане базисне рішення є допустимим (кутовий точкою) і невироджених. Використовуючи підхід 1, перейдемо до задачі мінімізації
За допомогою рівності (6.35) і (6.36) складаємо симплекс - таблицю, відповідну кутовий точці х 0:
Відповідно до п.4 алгоритму перевіряємо критерій оптимальності. В останньому рядку є негативні коефіцієнти. Виберемо з них найбільший по модулю (-3); другий стовпець дозволяє, змінна x2 перейде в основні (цей стовпець позначений стрілкою). Відповідно до п.5 знаходимо оцінні відносини і. Третій рядок є роздільною (відзначена горизонтальної стрілкою). На перетині дозволяють рядки і стовпці стоїть опорний елемент (обведений рамкою).
І т е р а ц і я 2. Будуємо таблицю за правилами п.6 алгоритму (табл. 6.10). У новому базисі основні змінні:.
Критерій оптимальності знов не знайдений. Тепер перший стовпець дозволяє; x1 - перехід в основні,; перший рядок роздільна, - опорний елемент.
Симплекс-таблиця для кутовий точки х 1
І т е р а ц і я 3. Нова симплексна таблиця набуде вигляду (табл. 6.11).
Симплекс-таблиця для кутовий точки х 2
І на цей раз критерій оптимальності не виконано; другий стовпець і другий рядок - дозволяють, - опорний елемент.
І т е р а ц і я 4. Переходимо до таблиці 6.12.
Симплекс-таблиця для кутовий точки х 3
Критерій оптимальності виконаний, отже f * = f (х *) = 24, оптимальне базисне рішення х * = (6,4,0,0,1,3).
Графічне рішення задачі представлено на рис. 6.10, звідки видно, що х * = (6; 4), і f * = f (х *) = 24.
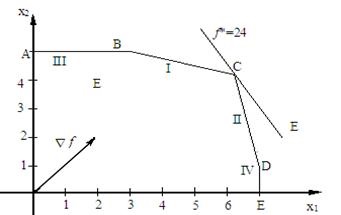
Мал. 6.10. Графічне рішення задачі 6.19