У ряді завдань математики і її додатків потрібно за відомим значенням тригонометричної функції знайти відповідне значення кута, виражене в градусної або в радіанної міру. Відомо, що одним і тим же значенням синуса відповідає безліч кутів, наприклад, якщо $ \ sin α = 1/2, $ то кут $ α $ може дорівнювати і $ 30 ° $ і $ 150 °, $ або в радіанної міру $ π / 6 $ і $ 5π / 6, $ і будь-якого з кутів, який виходить з цих додатком доданка виду $ 360 ° ⋅k, $ або відповідно $ 2πk, $ де $ k $ - будь-яке ціле число. Це стає зрозумілим і з розгляду графіка функції $ y = \ sin x $ на всій числовій прямій (див. Рис. $ 1 $): якщо на осі $ Oy $ відкласти відрізок довжини $ 1/2 $ і провести пряму, паралельну осі $ Ox, $ то вона перетне синусоїду в нескінченній множині точок. Щоб уникнути можливого різноманітності відповідей, вводяться зворотні тригонометричні функції, інакше звані круговими, або аркфункцій (від латинського слова arcus - «дуга»).
Основним чотирьом тригонометричним функціям $ \ sin x, $ $ \ cos x, $ $ \ mathrm \, x $ і $ \ mathrm \, x $ відповідають чотири аркфункцій $ \ arcsin x, $ $ \ arccos x, $ $ \ mathrm \ , x $ і $ \ mathrm \, x $ (читається: арксинус, арккосинус, арктангенс, арккотангенс). Розглянемо функції \ arcsin x і \ mathrm \, x, оскільки дві інші виражаються через них за формулами:
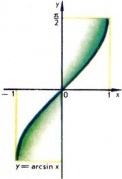
Рівність $ y = \ arcsin x $ за визначенням означає такий кут $ y, $ виражений в радіанної міру і укладений в межах від $ - \ frac $ до $ \ frac, $ синус якого дорівнює $ x, $ т. Е. $ \ sin y = x. $ функція $ \ arcsin x $ є функцією, зворотної функції $ \ sin x, $ розглянутої на відрізку $ \ left [- \ frac, + \ frac \ right], $ де ця функція монотонно зростає і приймає всі значення від $ -1 $ до $ + 1. $ Очевидно, що аргумент $ y $ функції $ \ arcsin x $ може приймати значення лише з відрізка $ \ left [-1, + 1 \ right]. $ Отже, функція $ y = \ arcsin x $ визначена на відрізку $ \ left [-1, + 1 \ right], $ є монотонно зростаючою, і її значення заполн яют відрізок $ \ left [- \ frac, + \ frac \ right]. $ Графік функції показаний на рис. $ 2. $
За умови $ -1 ≤ a ≤ 1 $ всі рішення рівняння $ \ sin x = a $ представимо у вигляді $ x = (- 1) ^ n \ arcsin a + πn, $ $ n = 0, ± 1, ± 2, .... $ Наприклад, якщо
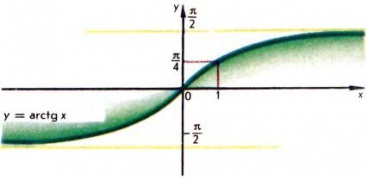
Співвідношення $ y = \ mathrm \, x $ визначено при всіх значеннях $ x $ і за визначенням означає, що кут $ y, $ виражений в радіанної мере, укласти в межах