Нехай n = 2m - парне число, а уi = f (xi) (i = 0..n) - значення функції у = f (x) для рівновіддалених точок a = x0. x1. x2. ..., xn = b з кроком h = (b-a) / n = (b-a) / 2m. На парі ділянок (рис.3) крива у = f (x) замінюється параболою у = L (x), коефіцієнти якої підібрані так, що вона проходить через точки у0. в1. у2.
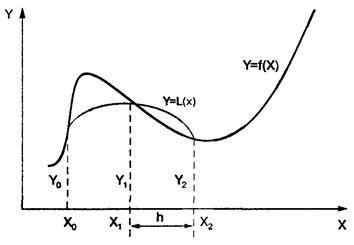
Рис.3 Геометрична інтерпретація інтегрування за методом Сімпсона.
Площа криволінійної трапеції, обмеженої зверху параболою, складе:
Підсумовуючи площі всіх криволінійних трапецій, одержимо:
Де p = 6-p, p = 4. Отже, формула Сімпсона для чисельного інтегрування має вигляд:
Остаточний член має вигляд:
На практиці для оцінки абсолютної похибки формули Сімпсона застосовують такі співвідношення:
При цьому, як правило, отримують для завищену оцінку.
2. Правило Рунге (n - парне) дає більш тонку оцінку:
Але при цьому може вийти для занижена оцінка, чого слід побоюватися.
Формули прямокутників і трапецій дають точне значення інтеграла, коли підінтегральна функція f (x) лінійна. бо тоді f "(x) = 0, а формула Сімпсона є точною для многочленів до третього ступеня. т. к. в цьому випадку f (4) = 0.
Якщо функція у = f (x) задана таблично і її похідні знайти важко, то в припустити жении відсутності швидко коливних складових можна застосувати наближені формули для похибок, виражені через кінцеві різниці:
1. Нехай потрібно обчислити інтеграл з точністю # 949 ;. Використовуючи формулу відповідного залишкового члена R, вибирають h таким чином, щоб виконувалася нерівність.
2. Подвійний перерахунок. (Правило Рунге).
ЧИСЕЛЬНЕ РІШЕННЯ трансцендентне і нелінійних рівнянь.
Якщо алгебраїчне або трансцендентне рівняння досить складне, то його коріння порівняно рідко вдається знайти точно. Тому великого значення набувають способи наближеного знаходження коренів рівняння і оцінки ступеня їх точності.
Процес знаходження наближених значень коренів рівняння:
де функція f (x) визначена і неперервна в деякому кінцевому або
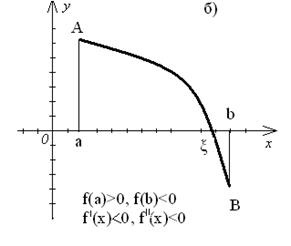
нескінченному інтервалі a Будь-яке значення # 955 ;, що звертає функцію f (x) в нуль, т. Е. Таке, що f (# 955;) = 0, називається коренем рівняння (1) або нулем функції f (x). Відокремити корені - це значить розбити всю область допустимих значень на відрізки, в кожному з яких міститься один корінь. Відділення коренів можна зробити двома способами - графічним і аналітичним. Графічний метод відділення коренів. a) будують графік функції у = f (x) для рівняння виду f (x) = 0. Значення дійсних коренів рівняння є абсциси точок перетину графіка функції у = f (x) з віссю Ох (рис.1); b) представляють рівняння (1) у вигляді # 966; (х) = g (x) і будують графіки функцій у = # 966; (х) і у = g (x). Значення дійсних коренів рівняння є абсциси точок перетину графіків функцій у = # 966; (х) і у = g (x) (рис.2). Відрізки, в яких укладено лише по одному кореню, легко знаходяться. Аналітичний метод відділення коренів заснований на наступній теоремі: якщо безперервна на відрізку функція приймає на кінцях відрізка значення різних знаків, тобто . то всередині цього відрізка знаходиться хоча б один корінь рівняння; якщо при цьому похідна зберігає знак всередині відрізка. то корінь є єдиним. Уточнення коренів до заданої точності. Тобто звуження відрізка локалізації кореня [a, b]. Розглянемо кілька методів. Метод половинного ділення (дихотомії). Нехай корінь відділений і належить відрізку. Знаходимо середину відрізка за формулою (рис.3). Якщо. то з - шуканий корінь. Якщо. то в якості нового відрізка ізоляції кореня вибираємо ту половину або. на кінцях якої приймає значення різних знаків. Іншими словами, якщо. то корінь належить відрізку. якщо - відрізку. Отриманий відрізок знову ділимо навпіл, знаходимо. Обчислюємо. вибираємо відрізок і т.д. Як тільки буде виконано. то в якості наближеного значення кореня, обчисленого з точністю. можна взяти . Після кожної ітерації відрізок, на якому розташований корінь зменшується вдвічі, тобто після n ітерацій він скорочується в 2 n раз. Таким чином, число ітерацій n в даному методі залежить від попередньо заданої точності # 949; і від довжини вихідного відрізка і не залежить від виду функції f (x). Це є важливою перевагою методу половинного ділення в порівнянні з іншими методами. Метод, однак, повільно сходиться при завданні високої точності розрахунку. Нехай на відрізку [a, b] функція f (x) неперервна і приймає на кінцях відрізка значення різних знаків, а похідні f '(x) і f "(x) зберігають постійний знак на інтервалі (a, b). Тоді можливі чотири випадки розташування дуги кривої (рис.4).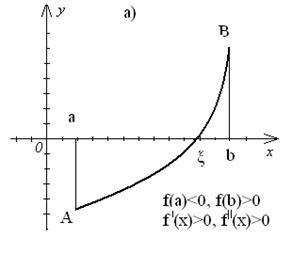
У методі хорд за чергове наближення беремо точку перетину з віссю Х прямий (рис.5), що з'єднує точки (a, f (a)) і (b, f (b))
Причому одна з цих точок фіксується - та, для якої знаки f (x) і f "(x) однакові.
Для рис.5 нерухомим кінцем хорди є х = a.
Рівняння хорди АВ:
Точка перетину хорди з віссю Х (у = 0):.
Тепер корінь знаходиться на відрізку [a, c1]. Замінюємо b на з1.
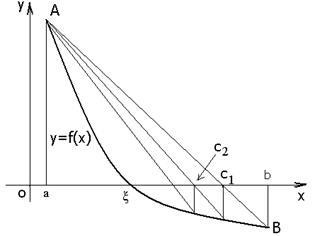
Рис.5. Ілюстрація методу хорд.
Застосовуючи метод хорд до цього відрізка, отримаємо:
Продовжимо і т.д. отримаємо: (2) Умова закінчення обчислень:
Для оцінки похибки можна користуватися загальною формулою:
Отже, якщо f (x) # 8729; f "(x)> 0, то наближене значення кореня знаходять за формулою (2), якщо f '(x) # 8729; f" (x) <0 (т.е. фиксируется х = b), то по формуле: